1  Elektromagnetische Größen

  • magn. Feldstärke \(H\) [A/m]
  • magn. Flussdichte \(B\) [Vs/m²] \(B=\mu H\) (oft “Magnetfeld”)
  • magn. Permeabilität \(\mu\) [Vs/Am] \(\mu=\mu_0\mu_r\) , \(\mu_0\)=4\(\pi\) 1e-7Vs/Am
  • mag. Suszeptibilität \(\chi_m=\mu_r\)-1
  • magn. Fluss \(\Phi\) [Vs]
  • spez. el. Widerstand \(\rho\) [\(\Omega\)m]
  • elektr. Feldstärke \(E\) [V/m]
  • dielektr. Verschiebung \(D\) [As/m²] \(D=\epsilon E\) (Hilfsfeld)
  • elektr. Permittivität \(\epsilon\) [As/Vm] \(\epsilon=\epsilon_0\epsilon_r\) , \(\epsilon_0\)=8.854e-12As/Vm
  • el. Suszeptibilität \(\chi_e=\epsilon_r\)-1
  • elektr. Stromdichte \(j\) [A/m²]
  • el. Leitfähigkeit \(\sigma\) [S/m]

1.1 Die Maxwell-Gleichungen

Faradaysches Induktionsgesetz

\[ \curl\vb E = -\pdv{\vb B}{t} \]

Ampèresches Durchflutungsgesetz

\[ \curl \vb H = \pdv{\vb D}{t} + \vb j \]

Die Quellen der Felder

Ladungsträger erzeugen eine elektrische Verschiebung \[\div \vb D = \varrho\]

Das Magnetfeld ist frei von Quellen und Senken \[\div \vb B = 0\]

Materialgleichungen: \(\vb B=\mu\vb H\), \(\vb D=\epsilon\vb E\), \(\vb j=\sigma\vb E\)

1.1.1 Amperesches Gesetz in der Geophysik

\[ \curl \vb H = \pdv{\vb D}{t} + \vb j \]

  • Wellenausbreitung \(\curl\vb H=\pdv*{\vb D}{t}\): Georadar
  • Induktion \(\curl\vb H=\vb j\), \(\curl\vb E=-\pdv*{\vb B}{t}\)
    Magnetotellurik, EMI in Zeit- und Frequenzbereich
  • Magnetostatik \(\curl\vb H=\vb j\), \(\curl\vb E=0\)

1.1.2 Näherungen und Methoden

\[ \curl \vb H = \pdv{\vb D}{t} + \vb j \qquad \curl\vb E = -\pdv{\vb B}{t} \]

Vorgänge/Felder \(\curl\vb H\) \(\curl\vb E\) Methoden
Stationär \(\vb j\) 0 Geoelektrik
Quasistationär \(\vb j\) \(-\pdv*{\vb B}{t}\) Induktion
Wellenvorgänge \(\pdv*{\vb D}{t}+\vb j\) \(-\pdv*{\vb B}{t}\) Georadar

1.2 Die Elektrische Leitfähigkeit

Elektrischer Widerstand
  • Länge \(L\), Querschnitt \(A\)
  • Spannung \(U\) [V], Stromstärke \(I\) [A]
  • Ohmscher Widerstand \(R\)=\(U\)/\(I\) [\(\Omega\)]
  • Stromdichte \(j\)=\(I\)/\(A\) [A/m²]
  • Elektr. Feld \(E\)=\(U\)/\(L\) [V/m]
  • Ohmsches Gesetz
    \(j=\sigma E\) (Leitfähigkeit \(\sigma\) [A/Vm])
    \(\Rightarrow \rho=1/\sigma=E/j\) [\(\Omega\)m] spezifischer Widerstand

\(\Rightarrow \rho = \frac{U/L}{I/A}=\frac{U}{I}\frac{A}{L}=R\cdot k\) Konfigurations-Faktor \(k\) [m]

1.3 Spezifischer Widerstand (Knödel, 2005)

25 Dekaden:

  • Diamant: 1e18 \(\Omega\)m
  • Kupfer: 1e-7 \(\Omega\)m

abhängig von:

  • Wassergehalt
  • Fluidleitfähigkeit
  • Tonanteil

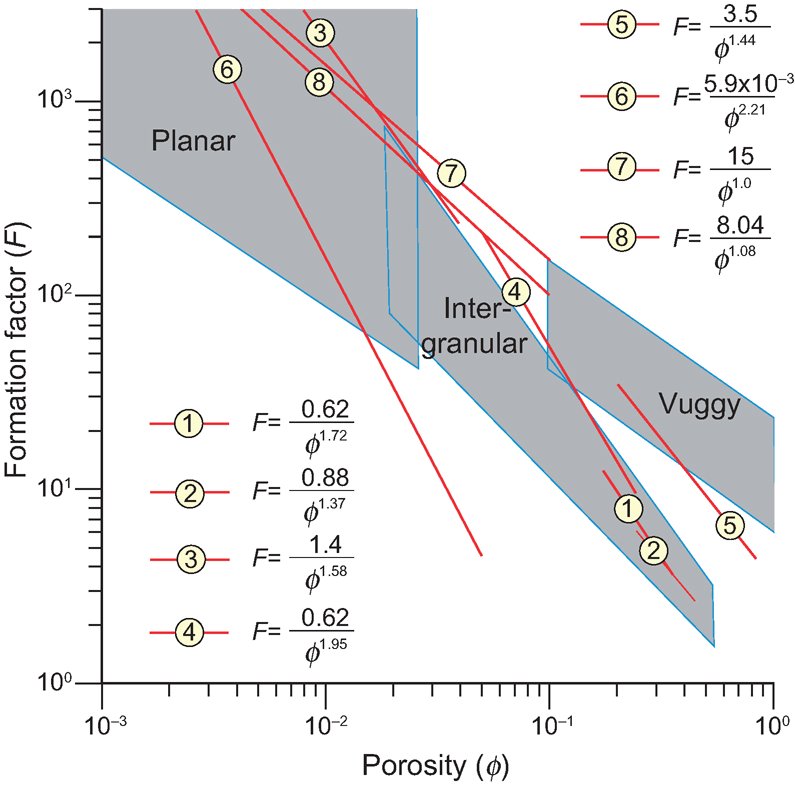
1.4 Archies Gesetz

Archies Gesetz

Der Formationsfaktor ist (bei tonfreien, gesättigten Sedimenten) exponentiell von der Porosität \(\phi\) abhängig. Der Exponent \(m\) heißt Zementationsexponent.

\[ F = \frac{\sigma_f}{\sigma}=\frac{\rho}{\rho_f} = \frac{a}{\phi^m} \]

  • negativer Anstieg im log-log-Plot

(Dentith und Mudge 2014)

1.5 Archies Gesetz II

Elektrische Leitfähigkeit des gesättigten (tonfreien) Porenraums:

\[ \sigma = \sigma_f / F = \sigma \phi^m S^n \quad \rho=\rho_f \phi^{-m} S^{-n}\]

  • \(\phi\)-Porosität
  • \(m\)-Zementationsexponent
  • \(S\)-Sättigung
  • \(n\)-Sättigungsexponent

Werte für \(m\):

  • unverfestigte Sedimente: 1.3
  • verfestigte Sedimente: 1.5-1.6
  • Sandsteine: 2.0

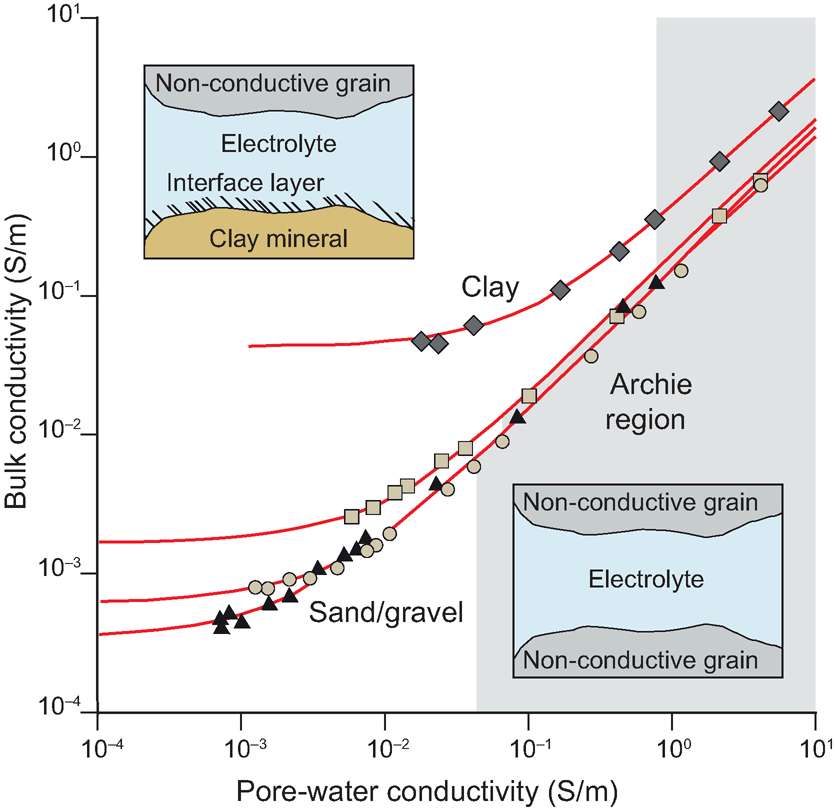
1.6 Grenzflächenleitfähigkeit

Bei kleinen Leitfähigkeiten

strebt die Leitfähigkeit gegen einen Grenzwert, die Grenzflächenleitfähigkeit

\[ \sigma = \sigma_f/F + \sigma_s \]

  • kleine Wasserleitfähigkeit
  • geringe Porosität
  • Tonminerale (Ton, Schluff)
  • metallische Partikel (Fe2/3)

1.6.1 Temperatur-Abhängigkeit

komplexe Abhängigkeit, aber Linearisierung um Temperatur \(T_0\) (meist 25°C)

\[ \sigma = \sigma_0 (1 + \alpha (T-T_0)) \]

\(\alpha\) - meist 0.02 (2% pro K)