6 Widerstandstomographie
6.1 Oberflächenmessungen
6.1.1 Klassische Mess-Abfolgen
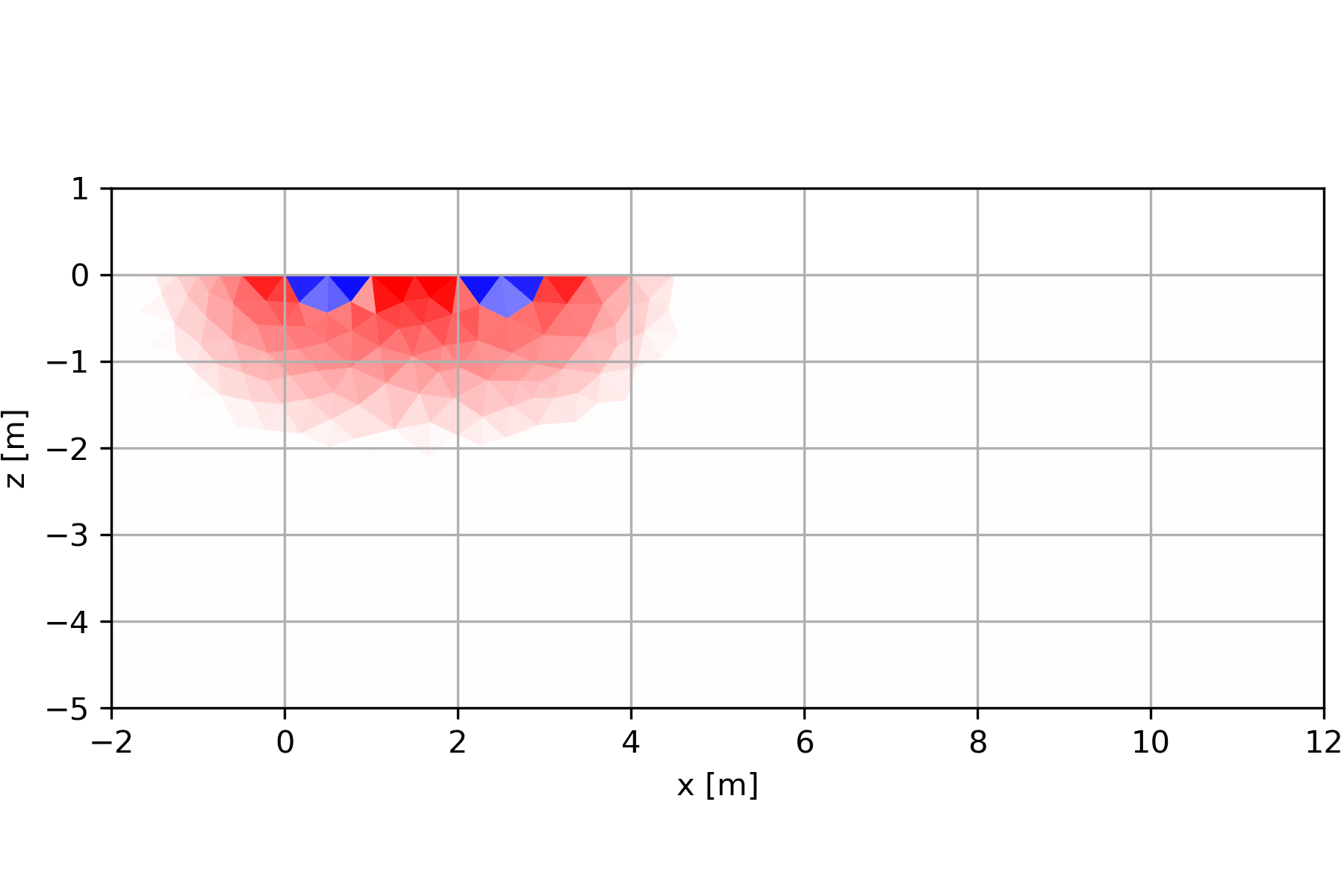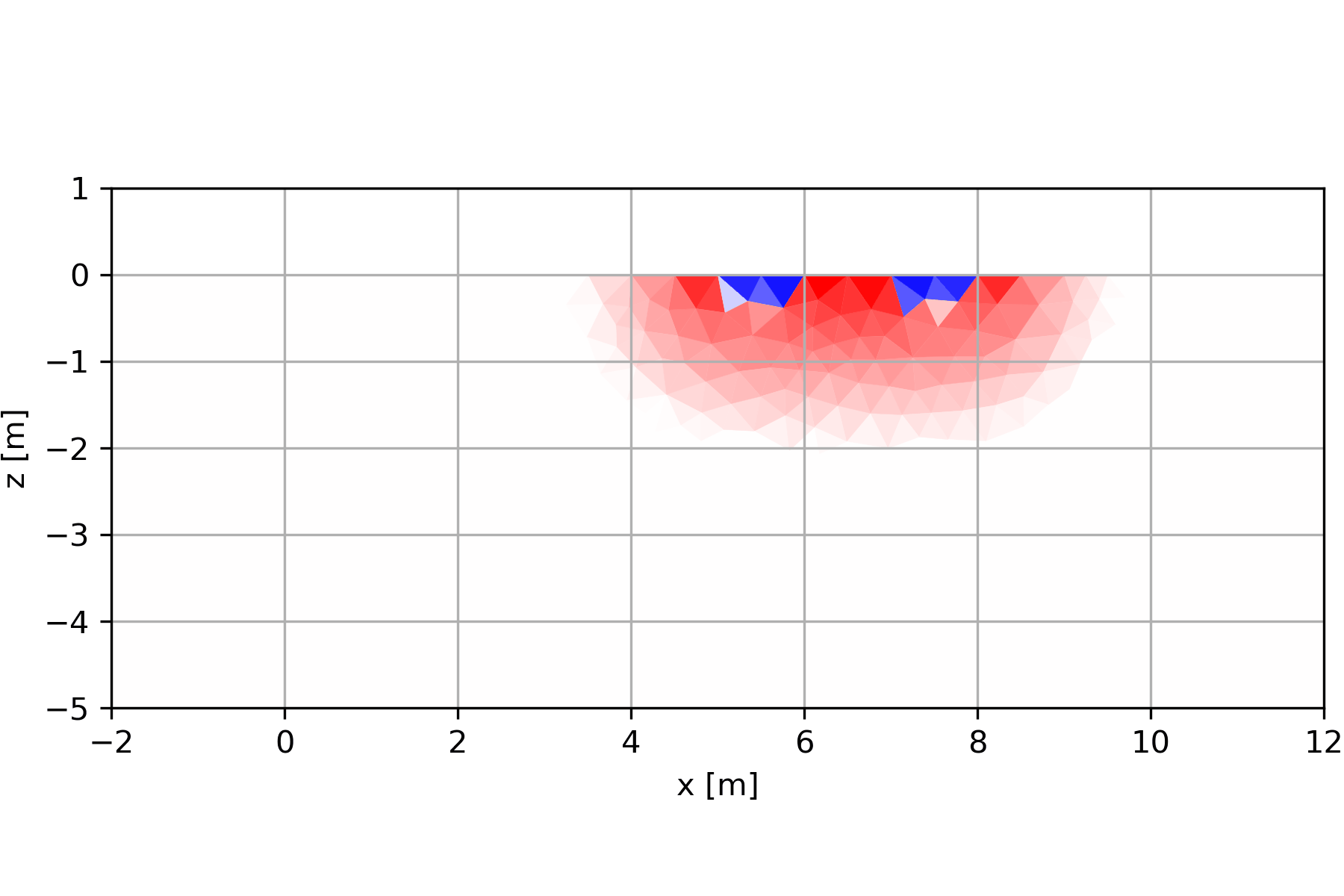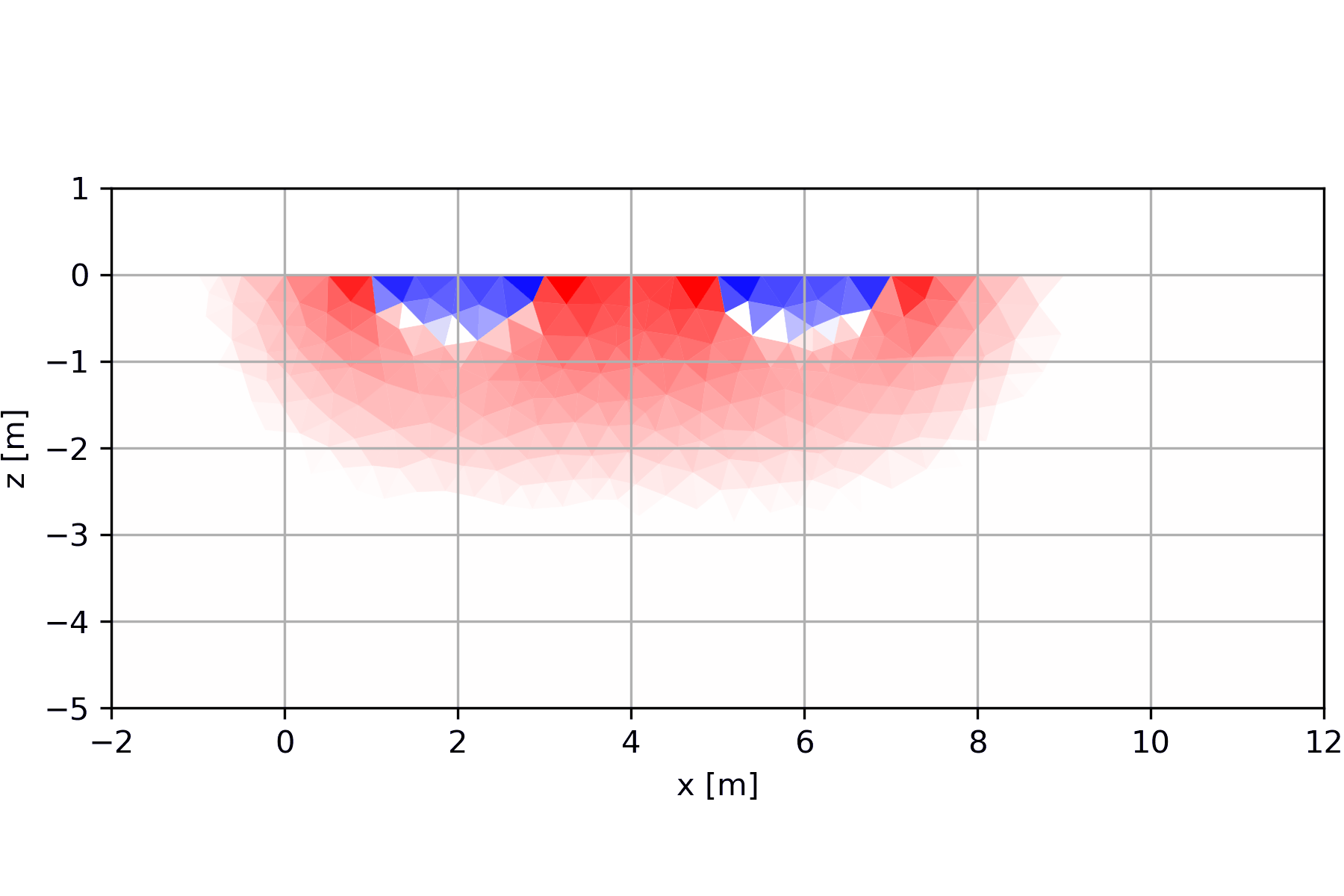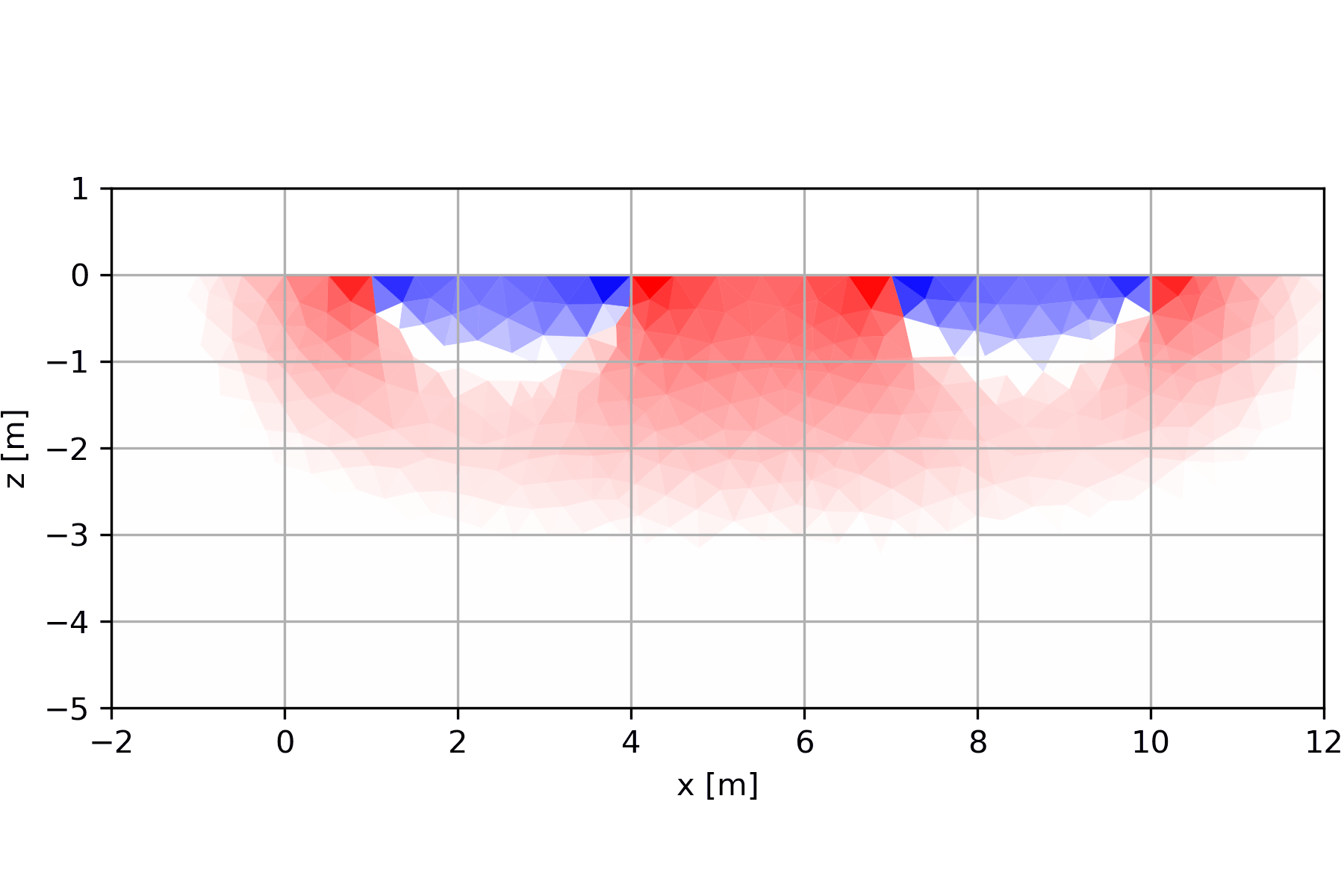
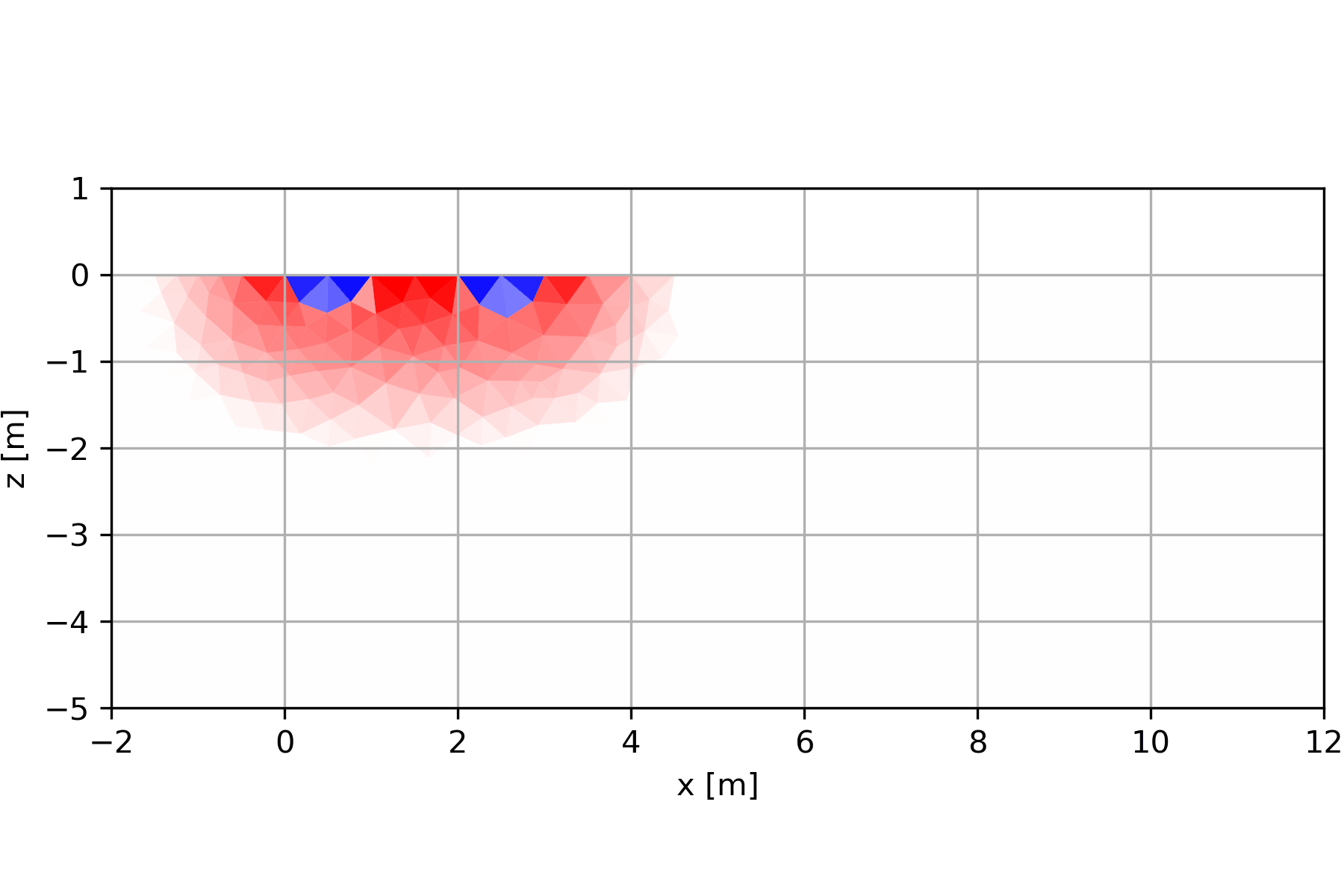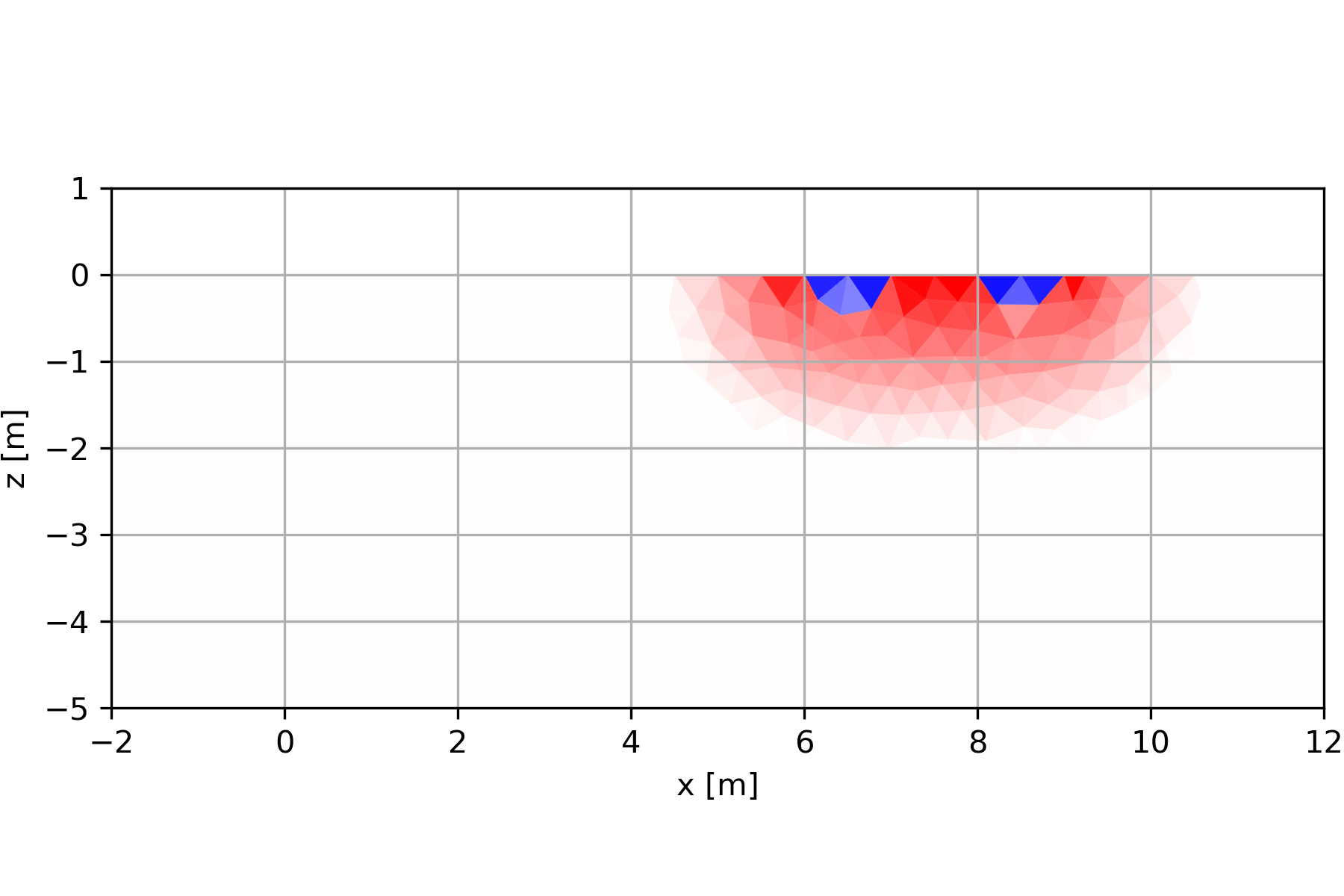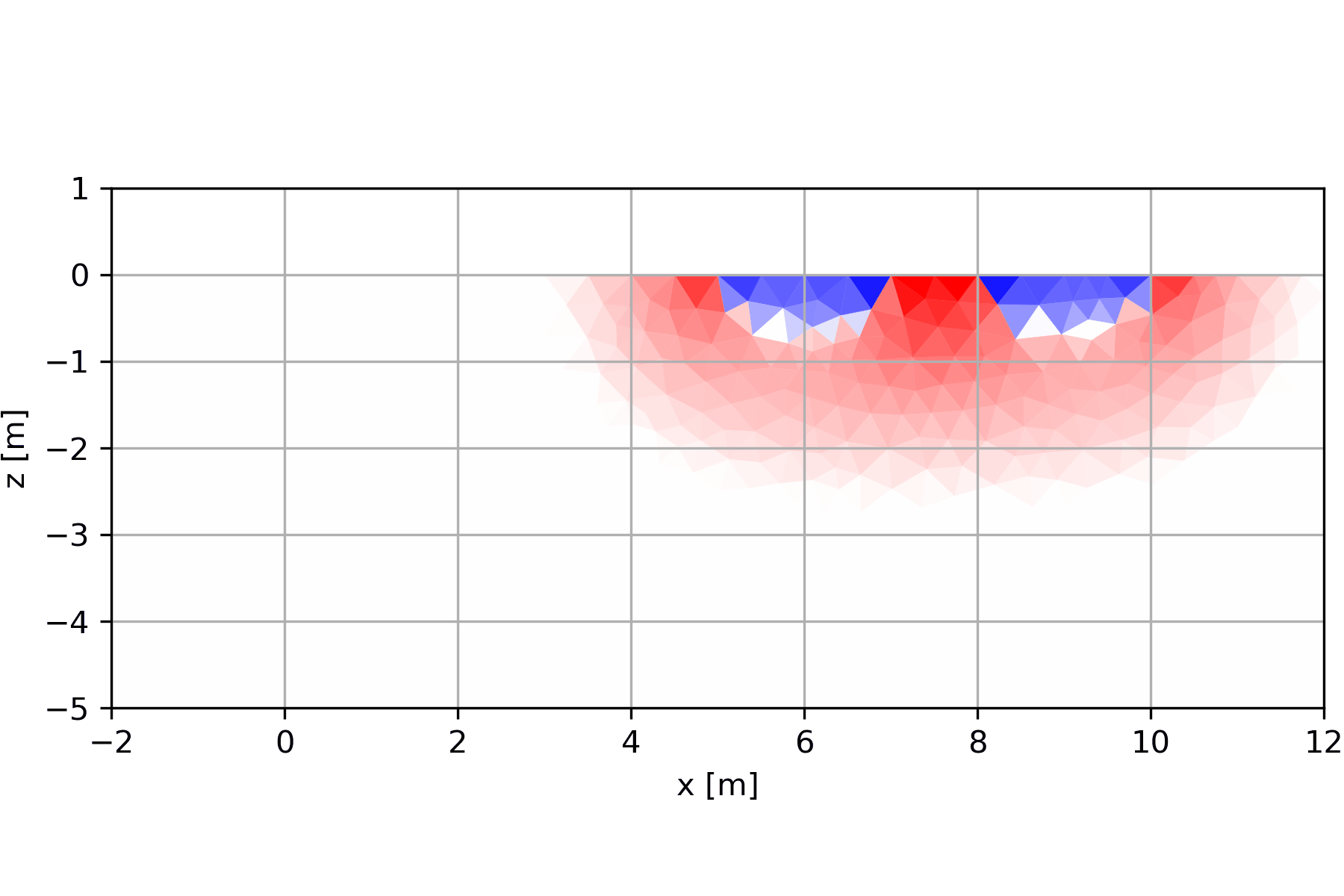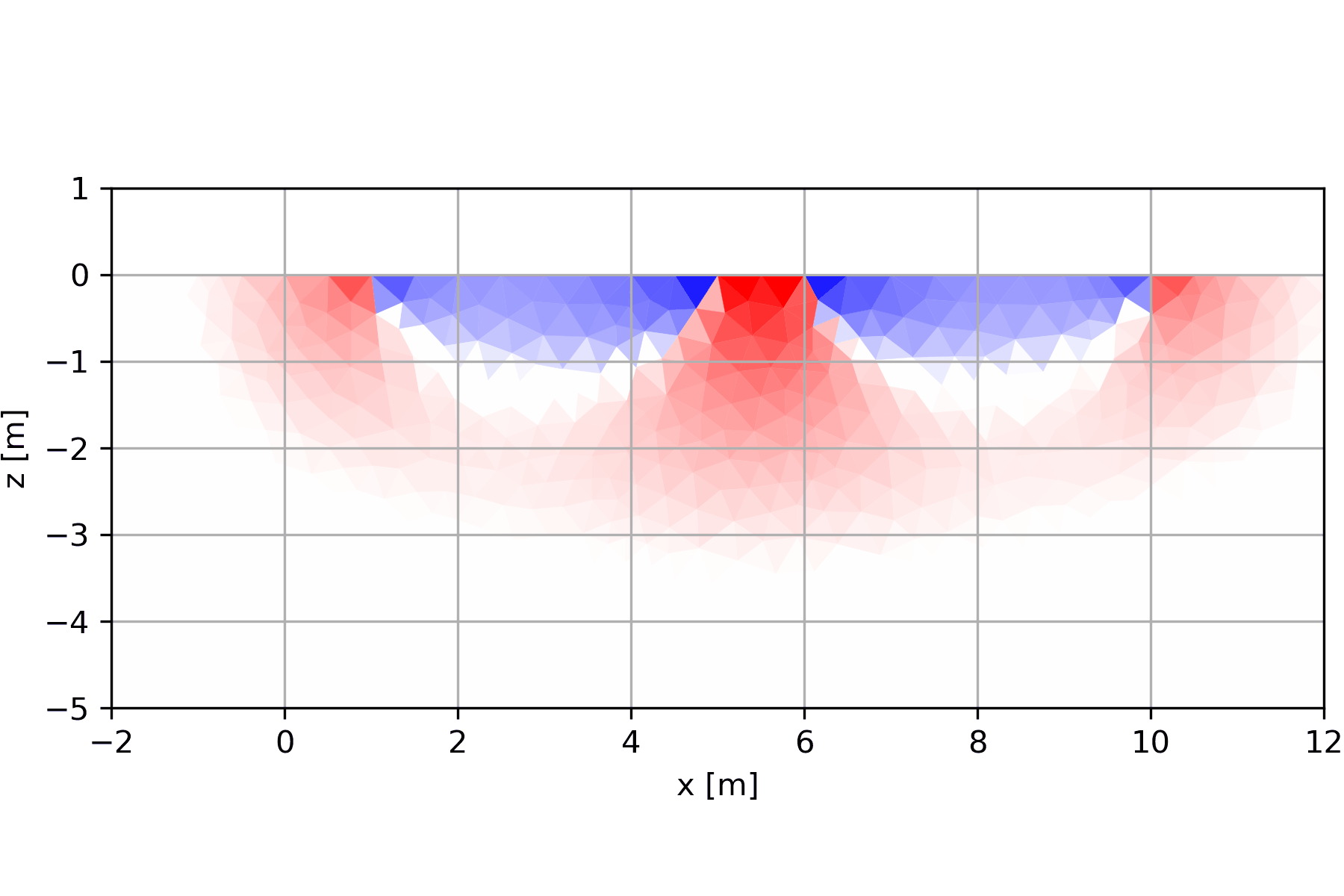
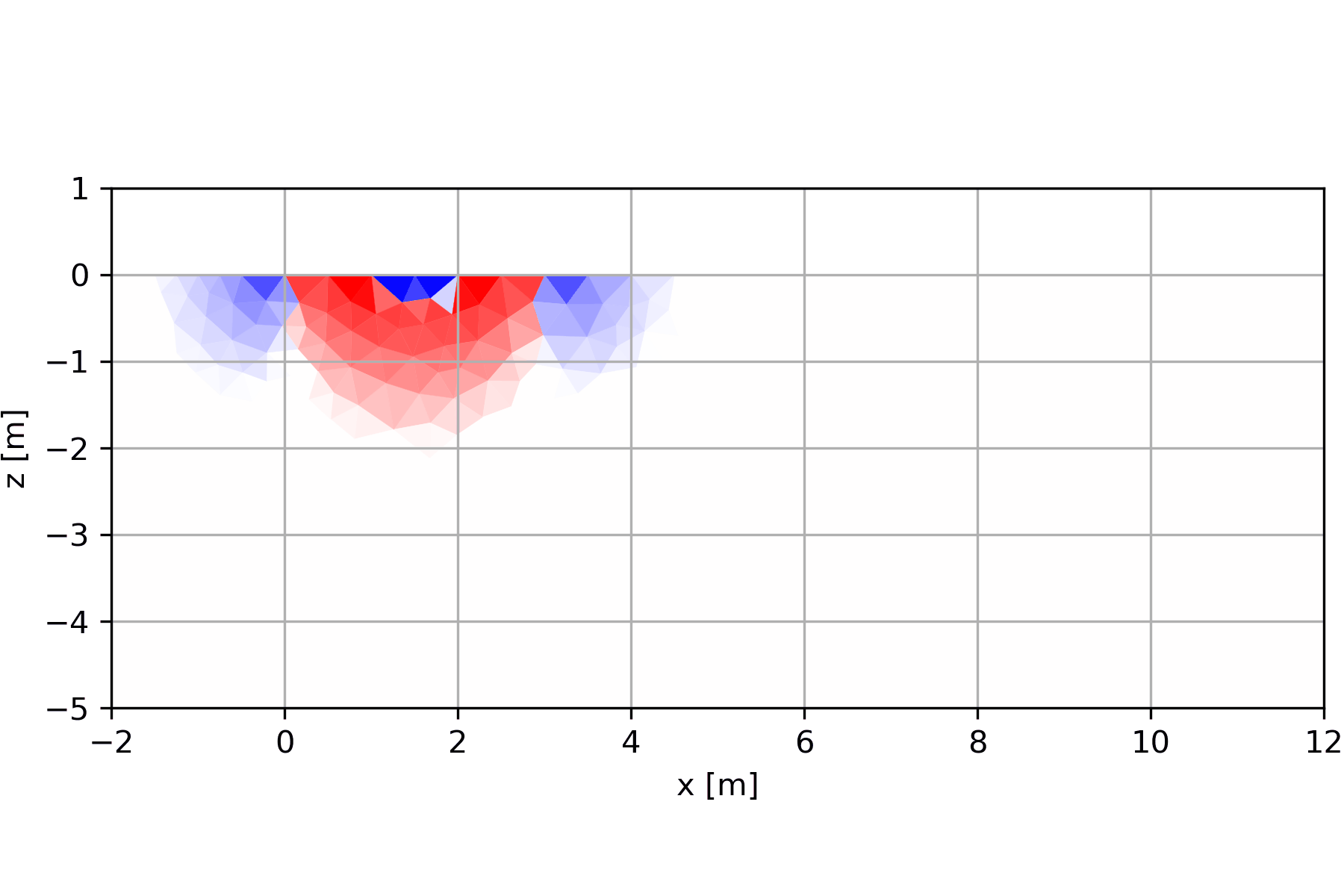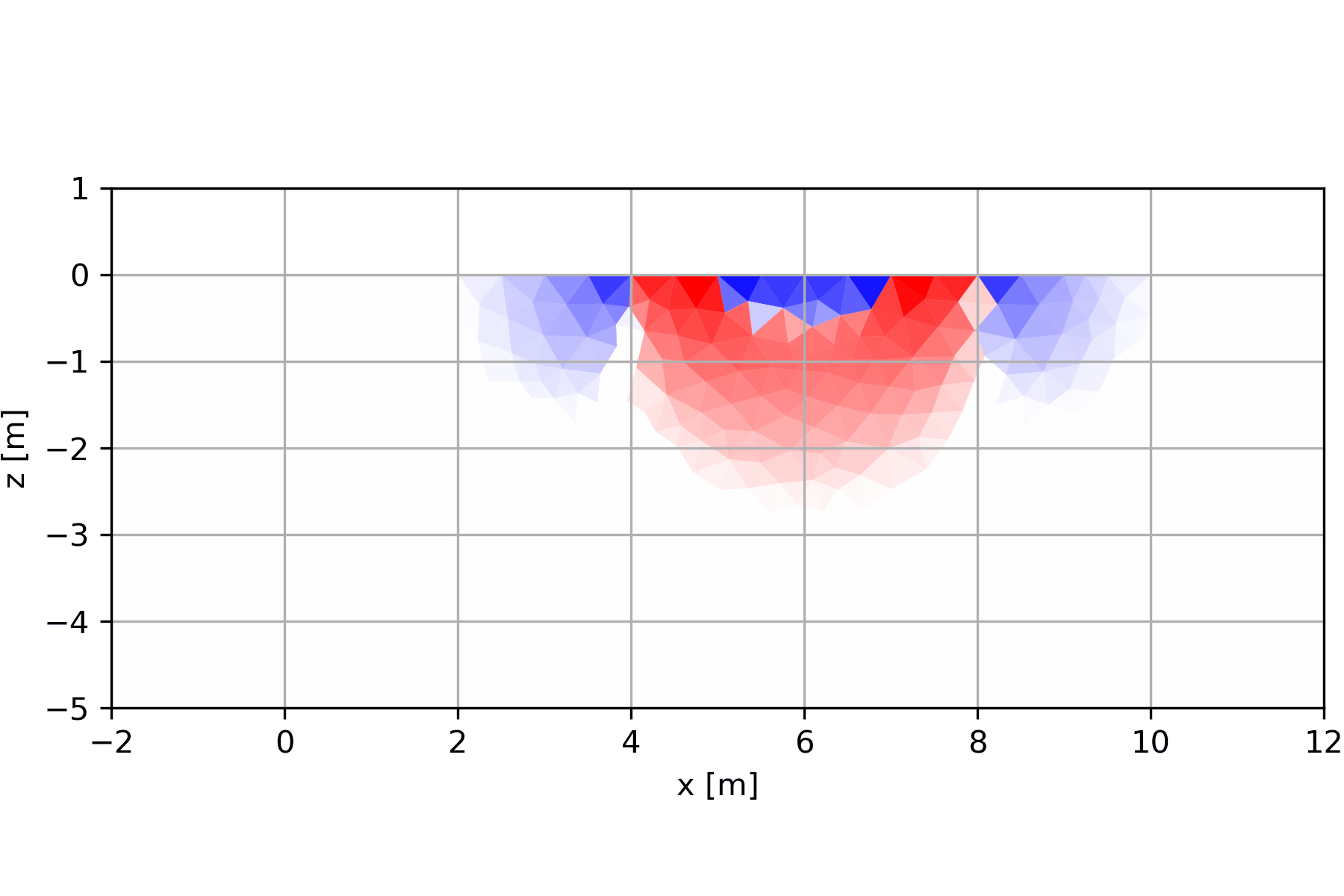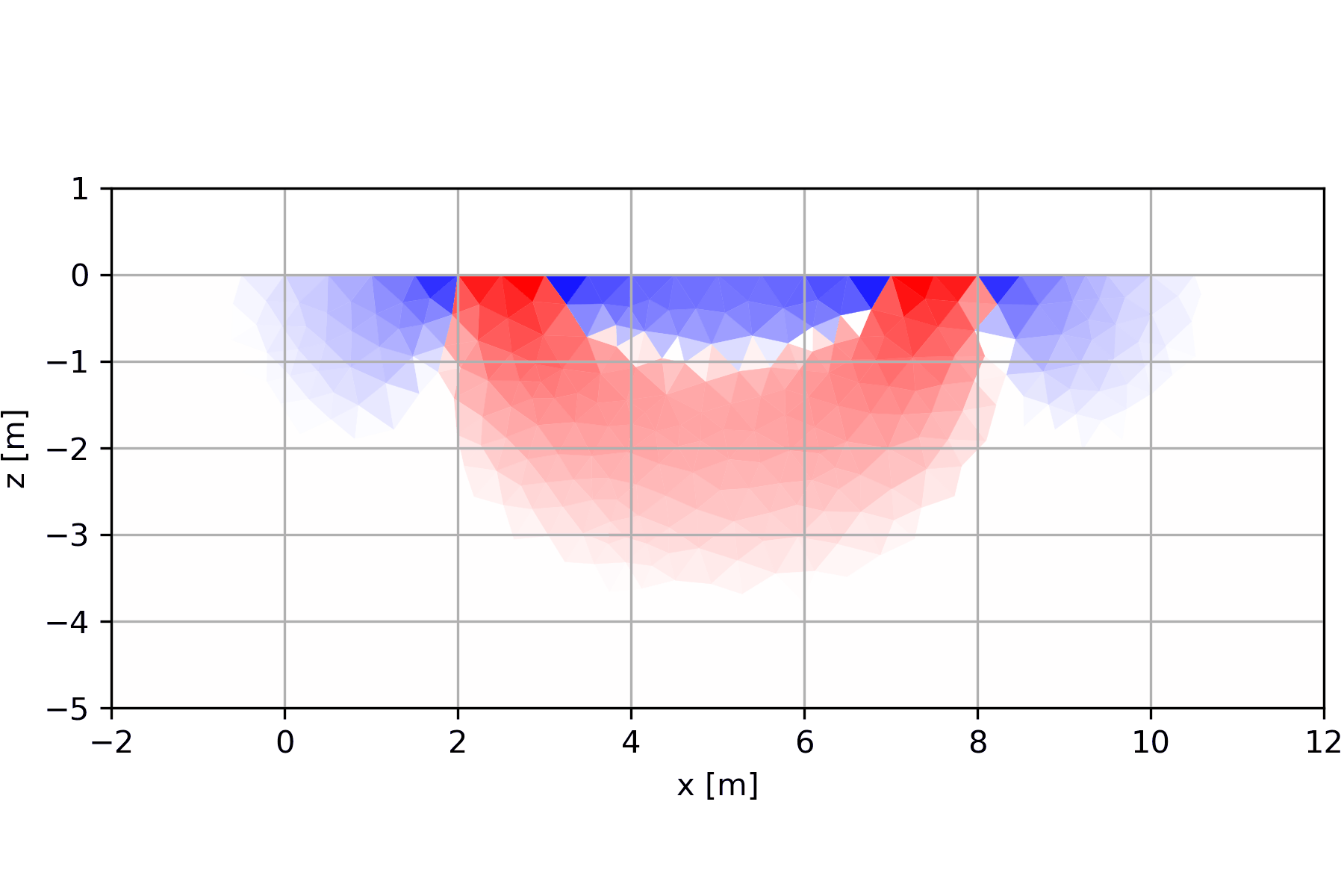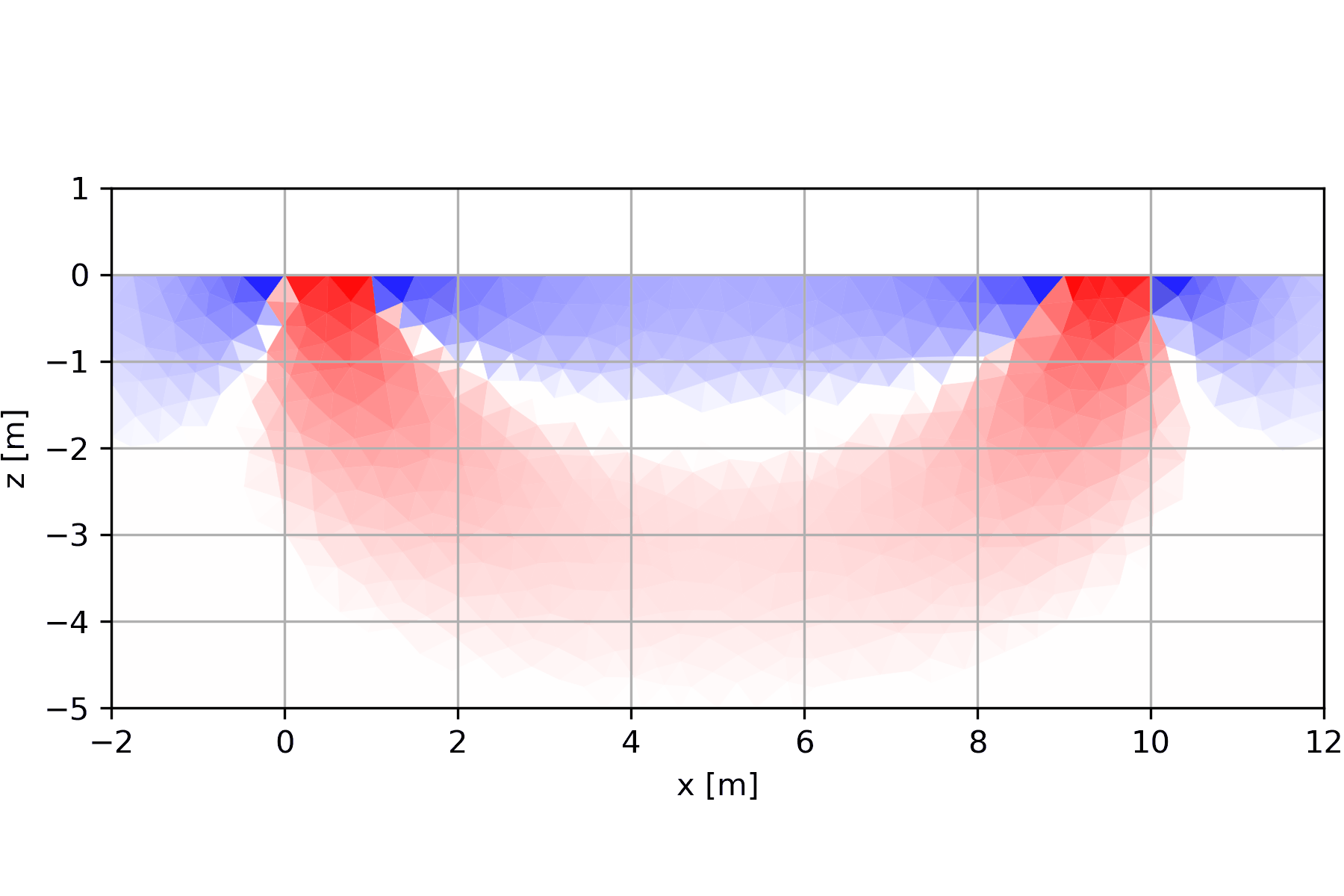
6.1.2 Entstehung der Pseudosektionen
6.1.2.1 Pseudosektion Wenner-Array
6.1.2.2 Pseudosektion Schlumberger-Array
6.1.2.3 Dipol-Dipol mit leitfähiger Einlagerung
6.1.2.4 Dipol-Dipol mit resistiver Einlagerung
6.2 Bohrlochgeoelektrik
Die Erdoberfläche stellt bei vergrabenen Elektroden einen Übergang zu einem schlechten Leiter da, wie wir ihn aus der Herleitung der Brechungsgesetze schon kennen.
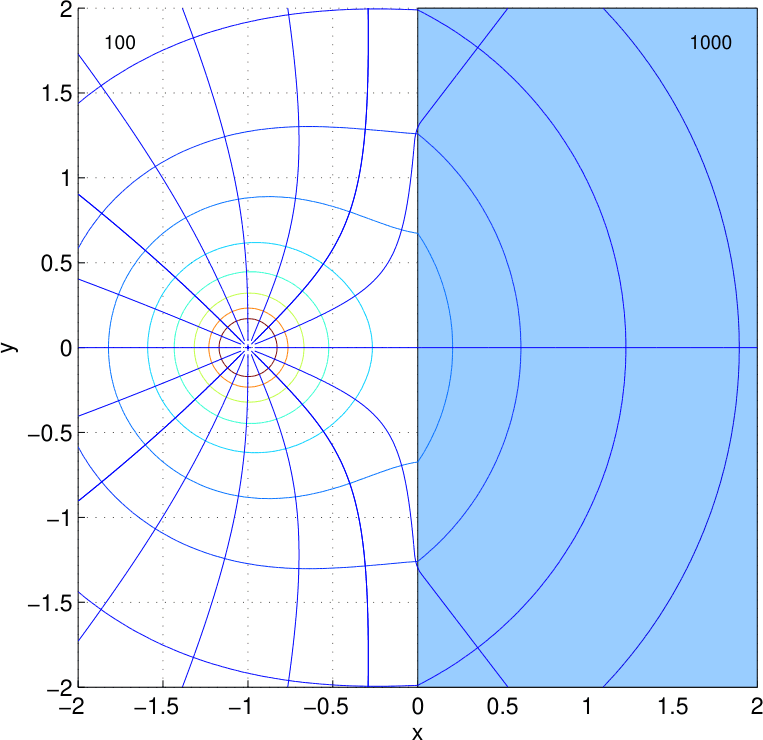
Allerdings können die Stromlinien nicht die Grenzfläche durchdringen, d.h. die Potentiallinien stehen senkrecht auf der Erdoberfläche.
6.2.1 Numerische Lösung und Geometrie-Faktor
Für eine Elektrode kennen wir bereits die Lösung im Vollraum:
\[u=\frac{\rho I}{4\pi |\vb r-\vb r_A|}\]
mit dem Geometriefaktor \(k=\frac{1}{4\pi |\vb r-\vb r_A|}\)
Um an der Erdoberfläche eine Normal-Komponente mit entgegengesetztem Vorzeichen zu erzeugen, benutzen wir eine Spiegelelektrode A’ (\(\vb r_A=[x, y, z]\)) an der Position \(\vb r_A'=[x, y, -z]\)$, die sich durch Spiegelung von A an der ebenen Grenzfläche ergibt. Diese erzeugt das Potential
\[u'=\frac{\rho I}{4\pi |\vb r-\vb r_A|}\]
Durch Superposition beider Potentiale ergibt sich \[u=\frac{\rho I}{4\pi |\vb r-\vb r_A|}+\frac{\rho I}{4\pi |\vb r-\vb r_A'|}\]
und daraus der Geometriefaktor \[k=\frac{1}{4\pi |\vb r-\vb r_A|}+\frac{1}{4\pi |\vb r-\vb r_A'|}\]
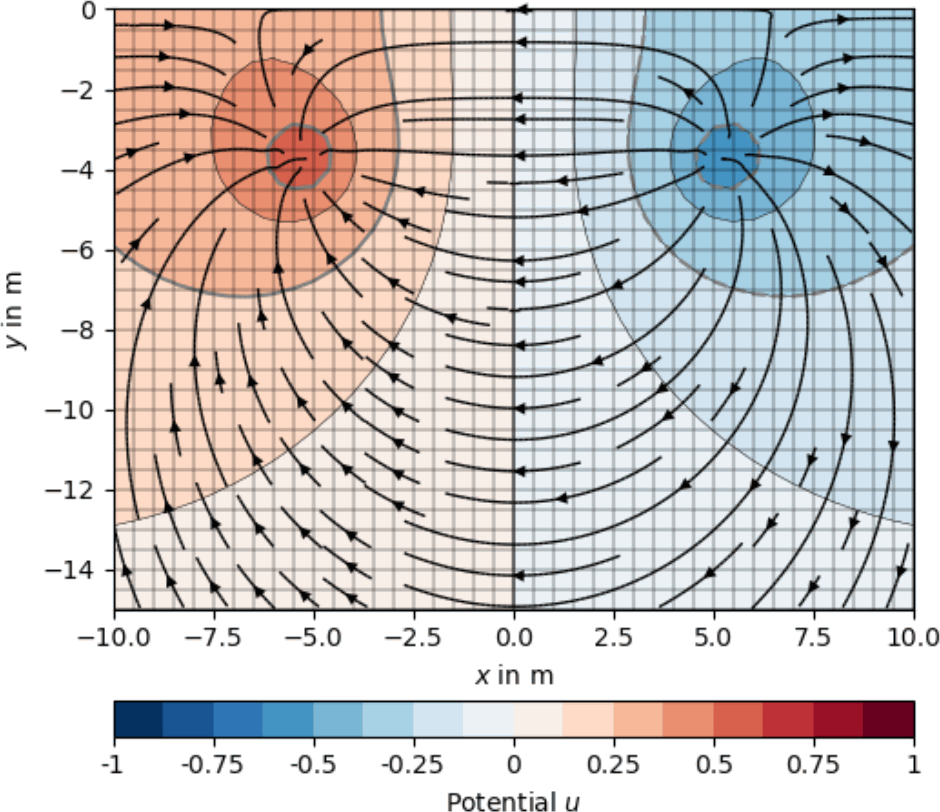
6.2.2 Potential und Stromlinien
Indem wir das für die zweite Stromelektrode B mit dem Spiegelpunkt B’ mit entgegengesetztem Vorzeichen wiederholen
\[u=\frac{\rho I}{4\pi |\vb r-\vb r_A|}+\frac{\rho I}{4\pi |\vb r-\vb r_A'|}-\frac{\rho I}{4\pi |\vb r-\vb r_B|}-\frac{\rho I}{4\pi |\vb r-\vb r_B'|}\]
erhalten wir die gewünschten Stromlinien, die entlang der Oberfläche fließen.
Wir setzen für \(\vb r\) die Positionen der Spannungselektroden M und N ein, und durch Umstellung ergibt sich der Geometriefaktor
\[k = \frac{4\pi}{\frac{1}{\overline{AM}}+\frac{1}{\overline{A'M}}-\frac{1}{\overline{AN}}-\frac{1}{\overline{A'N}}-\frac{1}{\overline{BM}}-\frac{1}{\overline{B'M}}+\frac{1}{\overline{BN}}+\frac{1}{\overline{B'N}}}\]
der allgemeingültig ist: Wenn A und B an der Erdoberfläche sind und A/A’ sowie B/B’ zusammenfallen, ergibt sich die bekannte Formel
\[ k = \frac{2\pi}{\frac{1}{\overline{AM}}-\frac{1}{\overline{AN}}-\frac{1}{\overline{BM}}+\frac{1}{\overline{BN}}} \]
6.2.3 Bohrloch-Geoelektrik
Elektroden werden selten “vergraben”, ein häufiger Einsatz ist aber mittels Bohrlöcher, wo Elektrodenkabel im Bohrlochfluid angekoppelt sind.
Genau wie bei Oberflächenmessungen kann man die 2D-Mess-Strategien in einzelnen Bohrlöchern anwenden. Daraus ergibt sich eine sehr ähnliche (Spiegelung an der Oberfläche muss beachtet werden) Sensitivitätsverteilung,
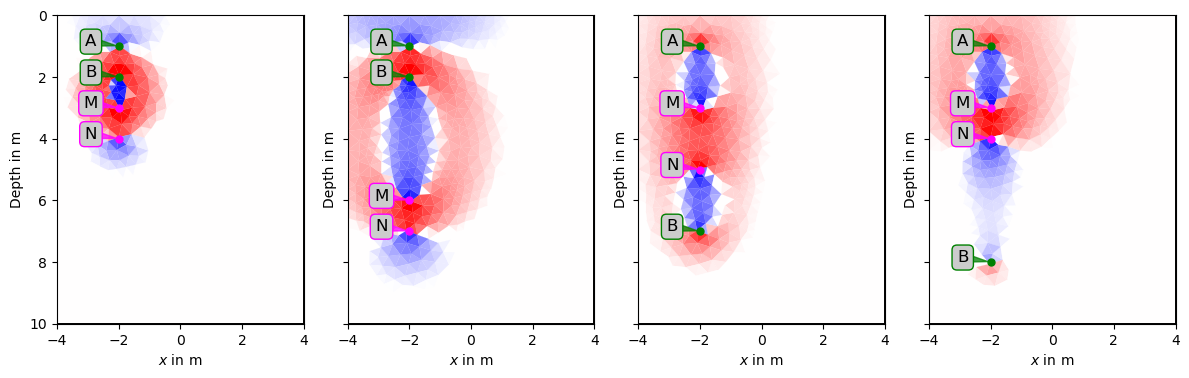
die allerdings jetzt rotationssymmetrisch um die Bohrlochachse ist. Mit größer werdenden Abständen erhält man Informationen aus größeren Abständen zum Bohrloch, kann aber nicht beurteilen, in welcher Richtung die Ursache einer Anomalie zu finden ist. Dazu benötigt man mehrere Bohrlöcher.
6.2.4 Crosshole-Geoelektrik
Hier werden Verteilung von Strom und Spannungselektroden auf zwei oder mehr Bohrlöcher verteilt. Nach der Aufteilung der Elektroden kann man die Anordnung Klassifizieren:
- Strom- und Spannungs-Elektroden in je einem Bohrloch
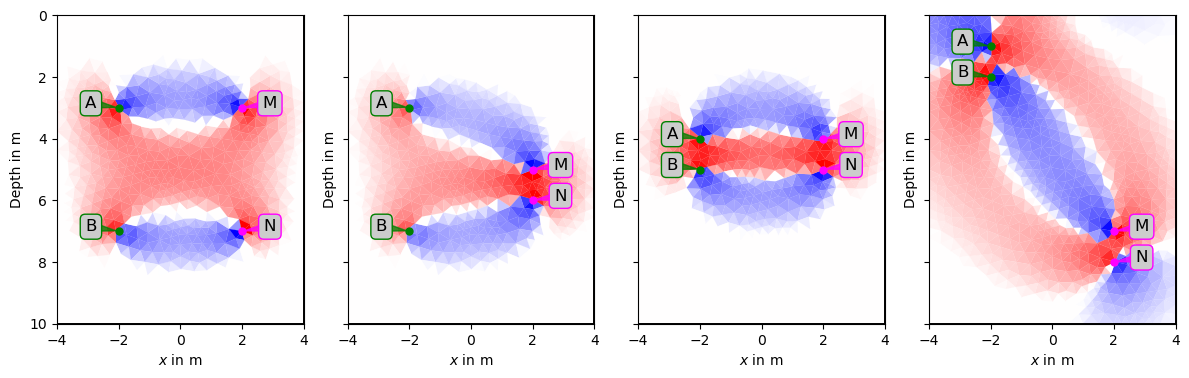
- je eine Strom- und Spannungs-Elektroden in einem Bohrloch
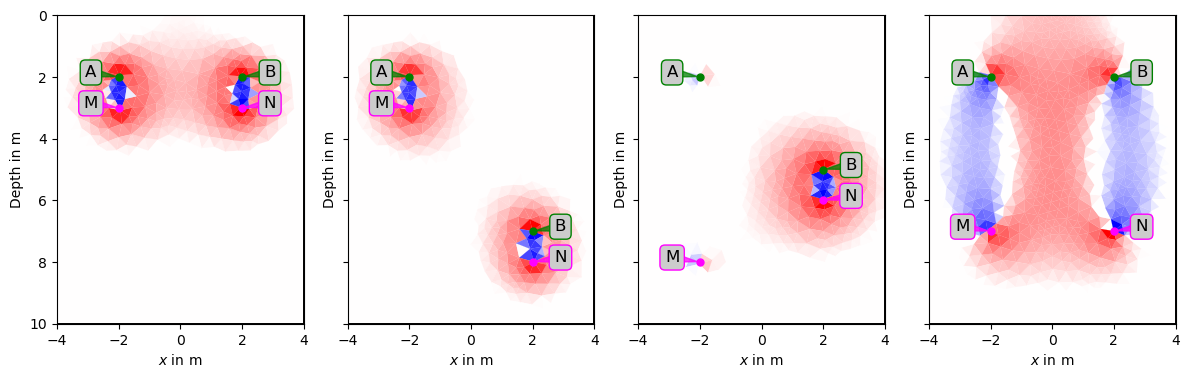
- eine einzelne Strom-(oder Spannungs)Elektrode in einem Bohrloch, die restlichen im zweiten
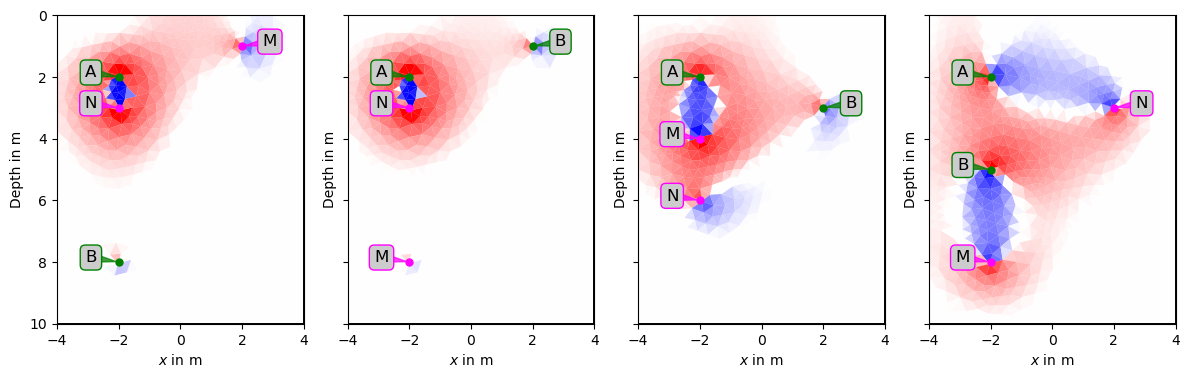
In Abhängigkeit vom Abstand der Elektroden und Bohrlöcher kann das Bohrlochfluid, welches sich in der Regel um den Formationsfaktor vom umliegenden Aquifer unterscheidet, einen großen Einfluss auf die Messergebnisse haben, der berücksichtigt werden muss (Doetsch u. a. 2010). Siehe auch 2D-Crosshole-Geoelektrik-Beispiel
6.3 3D-Geoelektrik
Prinzipiell lebt die Geoelektrik immer im dreidimensionalen Raum, da die Punktelektrode verhindert, dass Ableitung in senkrecht zur Mess-Ebene verschwinden. Entsprechend sind auch die Sensitivitätsfunktionen dreidimensional und werden lediglich für die Inversion entlang der Senkrechten integriert.
Die Sensitivität einer linearen Anordnung ist rotationssymmetrisch zur Mess-Linie. Daher können wir nicht unterscheiden, ob sich eine Anomalie in der Tiefe, vor oder hinter einem Profil befindet. Dazu werden weitere parallel oder besser noch senkrechte Profile benötigt, die den 3D-Raum abdecken.

3D-Inversion von 2D-Profilen
3D-Auslage
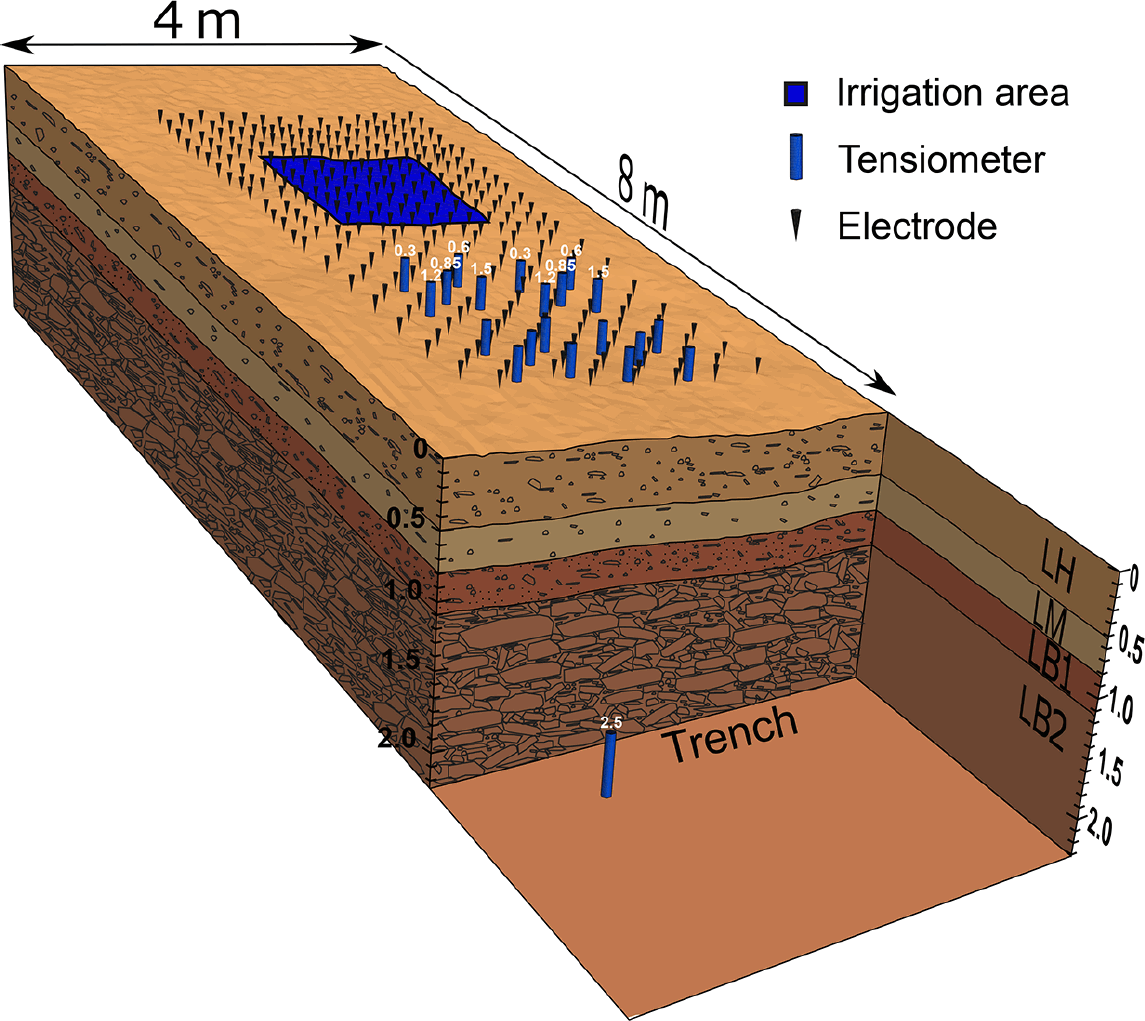
Garre, Bechtold,
6.3.1 3D Crosshole surveys
6.4 Modellierung & Inversion
6.4.1 Vorwärtsrechnung
Die Simulation von Messungen auf Basis einer Leitfähigkeitsverteilung erfordert die numerische Lösung der partiellen Differentialgleichung
\[ -\nabla \cdot \sigma \grad u = \delta(\vb r - \vb r_s) \]
Dazu existieren verschiedene Techniken angewendet:
- die Finite-Differenzen-Methode nähert die Ableitungen durch Differenzenquotienten
- die Finite-Element-Methode nähert die Potentialverteilung durch Superposition von Ansatzfunktionen
Beide Methoden erfordern die Diskretisierung des Untergrunds mit Rechtecken oder Dreiecken (2D), Quadern, Prismen oder Tetraedern (3D).
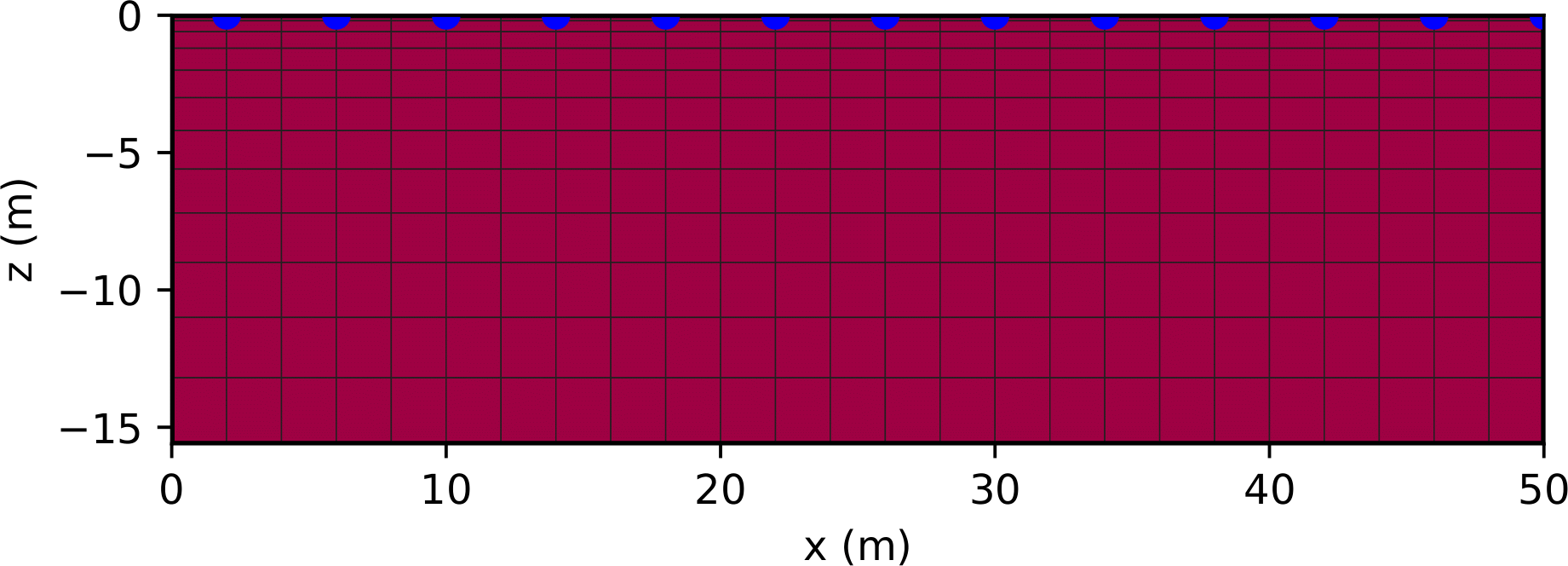
Die Methoden der Modellierung werden beschrieben durch Rücker u. a. (2006) und sind implementiert in pyGIMLi (Rücker u. a. 2017). Siehe auch 2D-ERT-Modellierungsbeispiel
6.4.2 Inversion
Aufgabe der Inversion ist die Bestimmung einer Parameterverteilung (hier: spez. Widerstand), welche die Daten im Rahmen einer bestimmten Genauigkeit erklären kann. Dazu wird ein Startmodell (meist homogen) iterativ verbessert, bis die Vorwärtsantwort mit den Daten im Rahmen der Fehler überein stimmt. Dabei werden die Sensitivitäten verwendet.
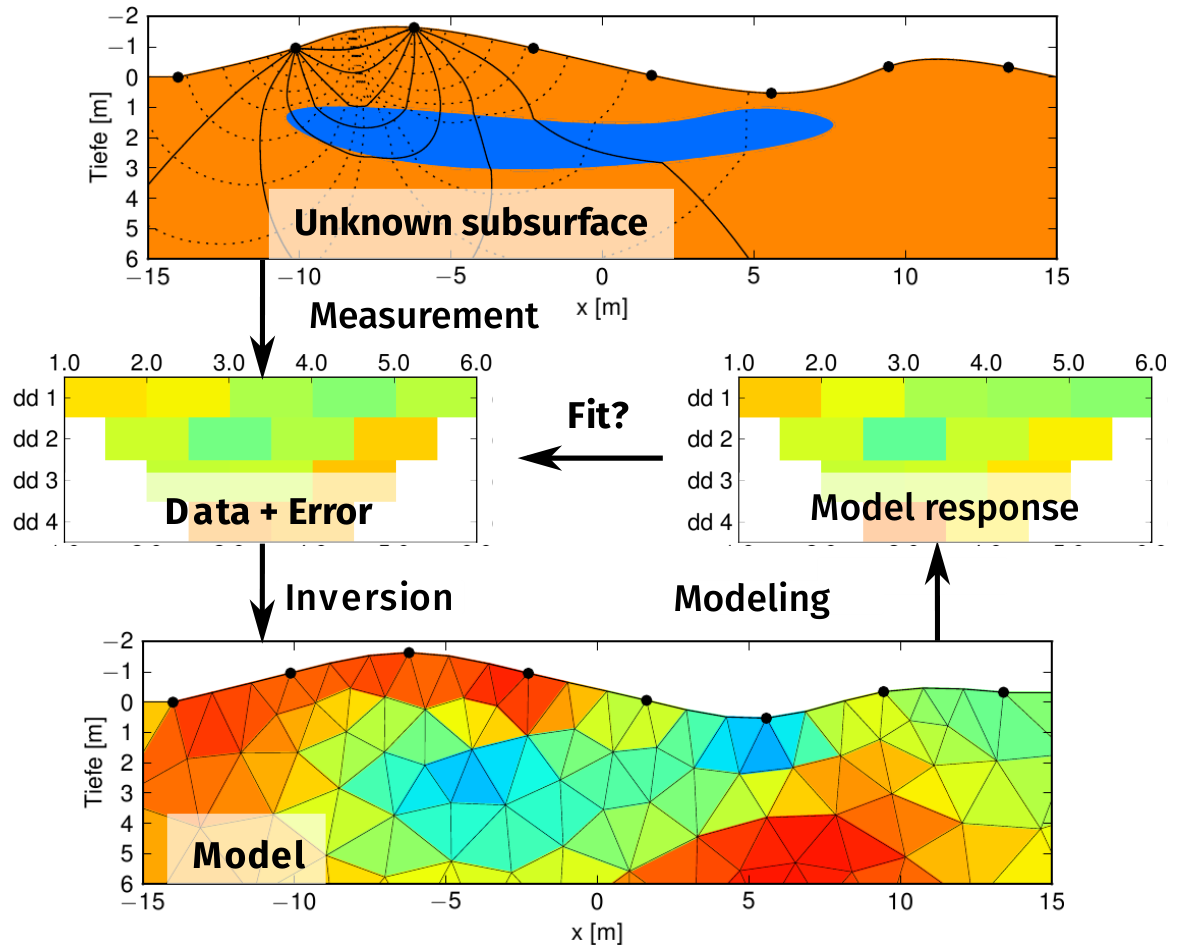
6.4.3 Inversion - Methodik
Datenvektor \(\vb d=\{d_i\}=\{\rho^a_i\}\), Modellvektor \(\vb m=\{m_j\}=\{\rho_j\}\)
Datenmisfit \(\vb \delta \vb d = \vb d - \vb f(\vb m)\) soll klein sein (Quadrate)
Modellveränderung \(\delta\vb m\) über Sensitivitätsmatrix \(S_{i,j}=\pdv{f_i(\vb m)}{m_j}=\pdv{\rho_a(\rho)}{\rho}\)
\[\Rightarrow \vb S \vb \delta \vb m = \delta \vb d\]
Least-SquaresLösung \(\vb S^T \vb S \delta \vb m=\vb S^T \delta \vb d\) +Zusatzterme
Die konkrete Methodik wird durch Günther u. a. (2006) beschrieben. Bevorzugt wird eine Diskretisierung mit Dreiecken (2D) bzw. Tetraedern (3D) eingesetzt, weil damit beliebige Geometrien, z.B. Topographie(e.g., Udphuay u. a. 2011), nachgebildet werden können und die Zellgröße auflösungsangepasst gewählt werden kann. Zur Bestimmung des Daten-Fehlers kann die sogenannte Normal-Reziprok-Methode, eine statistische Analyse des Unterschieds zwischen Hin- und Rück-Messungen und Ableitung eines Fehlermodells durchgeführt werden (Udphuay u. a. 2011). Siehe auch pyGIMLi-Beispiel.
2D Inversion

6.5 Ausgedehnte Elektroden
- Vereinfachtes Modell: Punktförmige Stromeinspeisung \(j=I\frac{\vb r}{r^3}\)
- Endliche Elektroden: Verteilung des Stroms auf Fläche
- Plattenelektroden, Linienelektroden, Ringelektroden
- (Halb)Kugel-förmige Elektroden: identische Lösung im Außenraum
6.5.1 Nicht-Punkt-Elektroden
Das Complete Electrode Model (CEM)
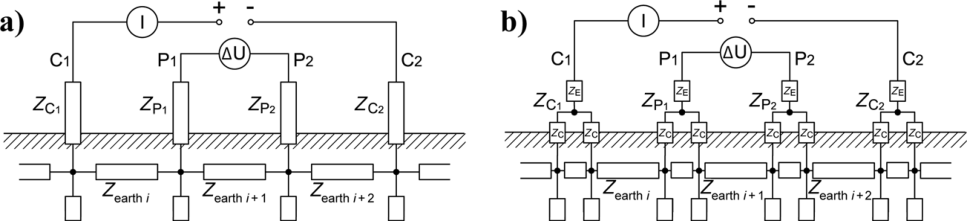
Zusätzliche Gleichungen: \(z_l\sigma\pdv{u}{n} + u = U_l\) auf \(\Gamma_l\) und \(\int_{\Gamma_l}\sigma \pdv{u}{n}ds=I\)
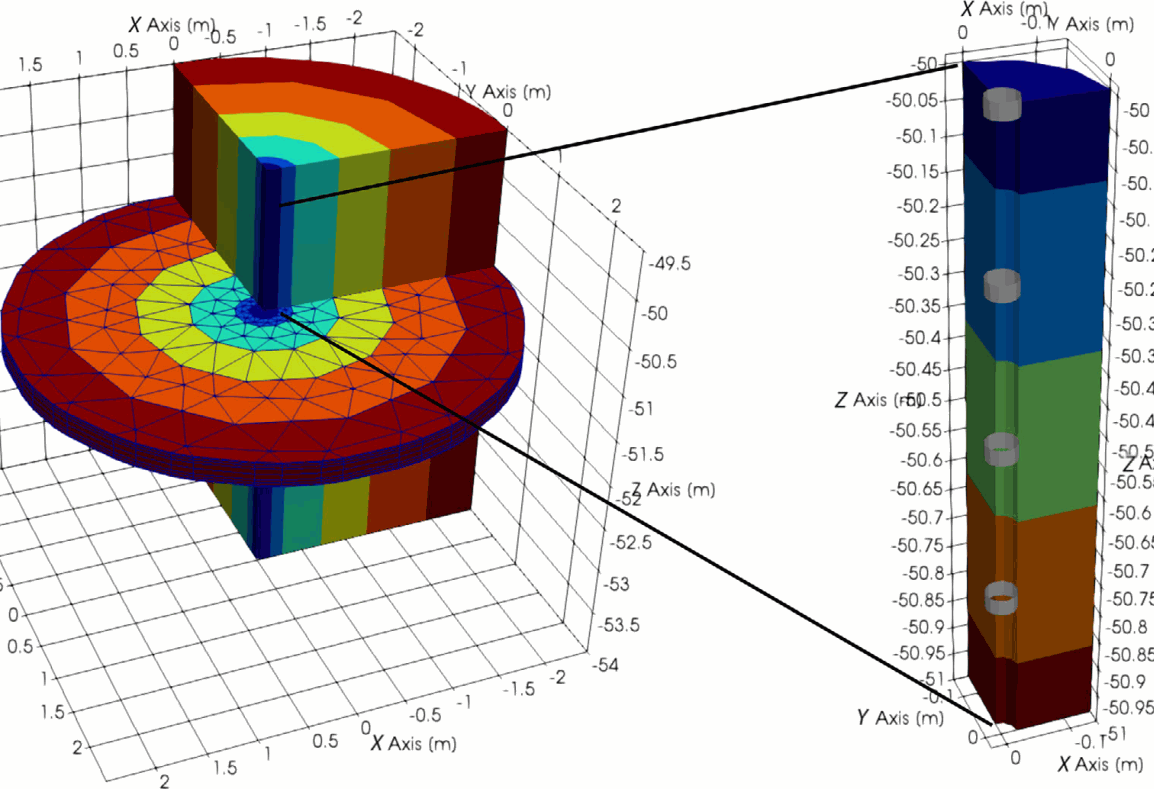
6.5.2 Modellierung von langen Elektroden
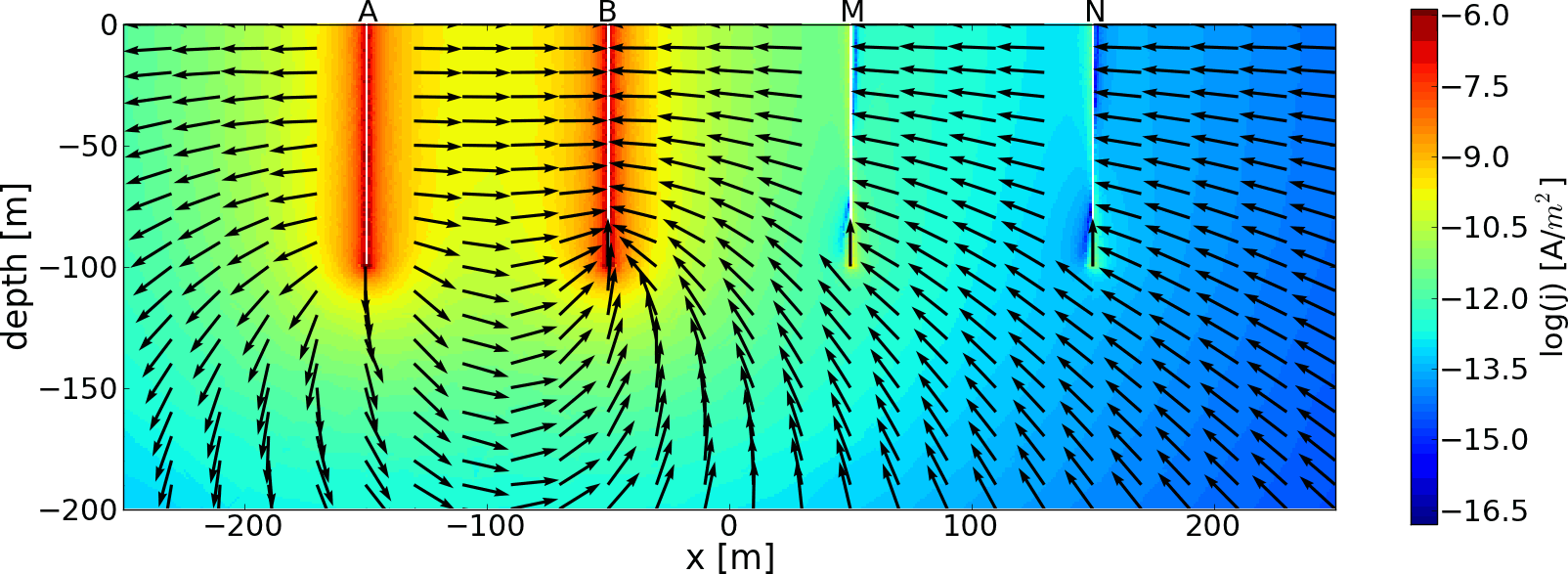
6.5.3 Einfluss der Stecktiefe
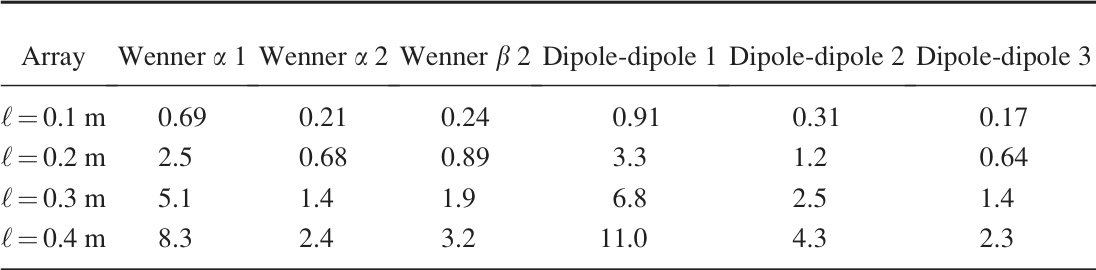
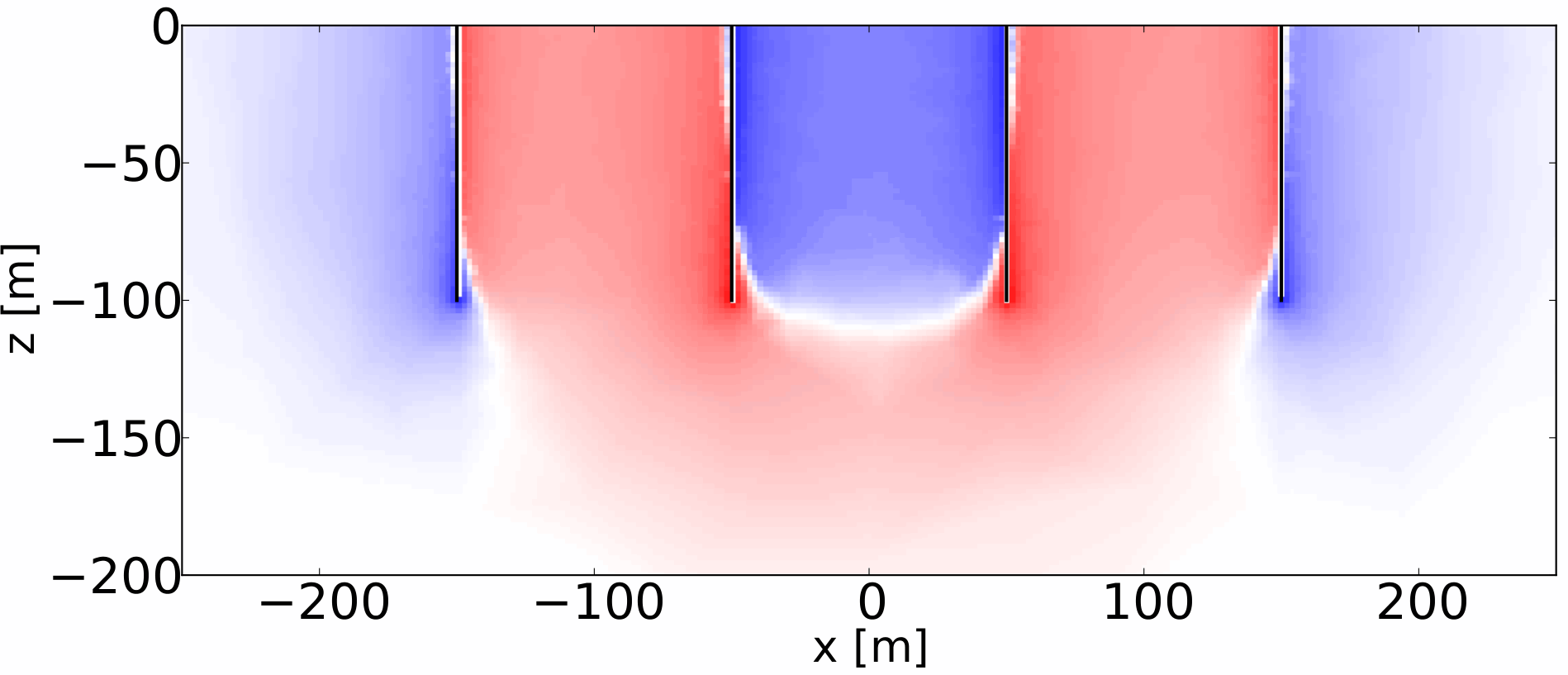
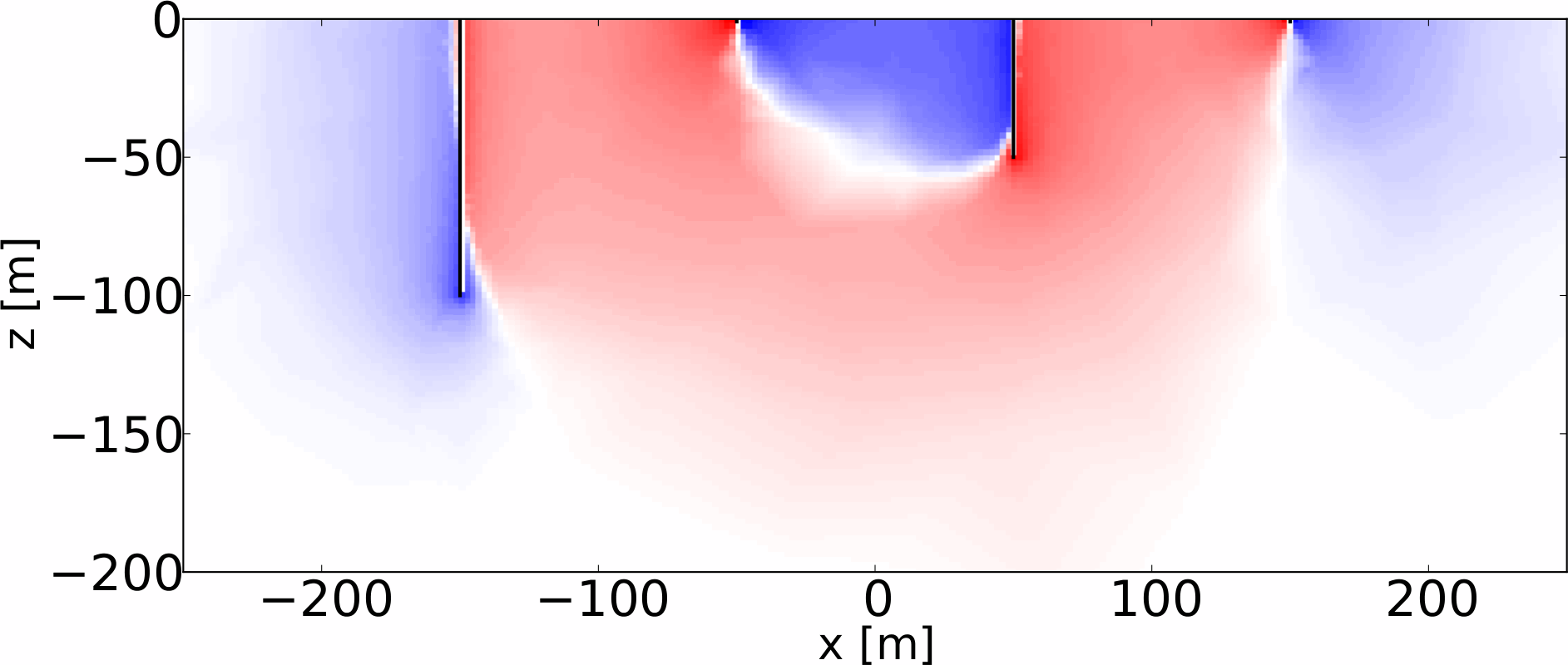
6.5.4 Langelektroden - Stromdichte
6.5.5 Langelektroden - Sensitivitäten
6.5.6 Lang-Elektroden-Geoelektrik (SaMoLEG)
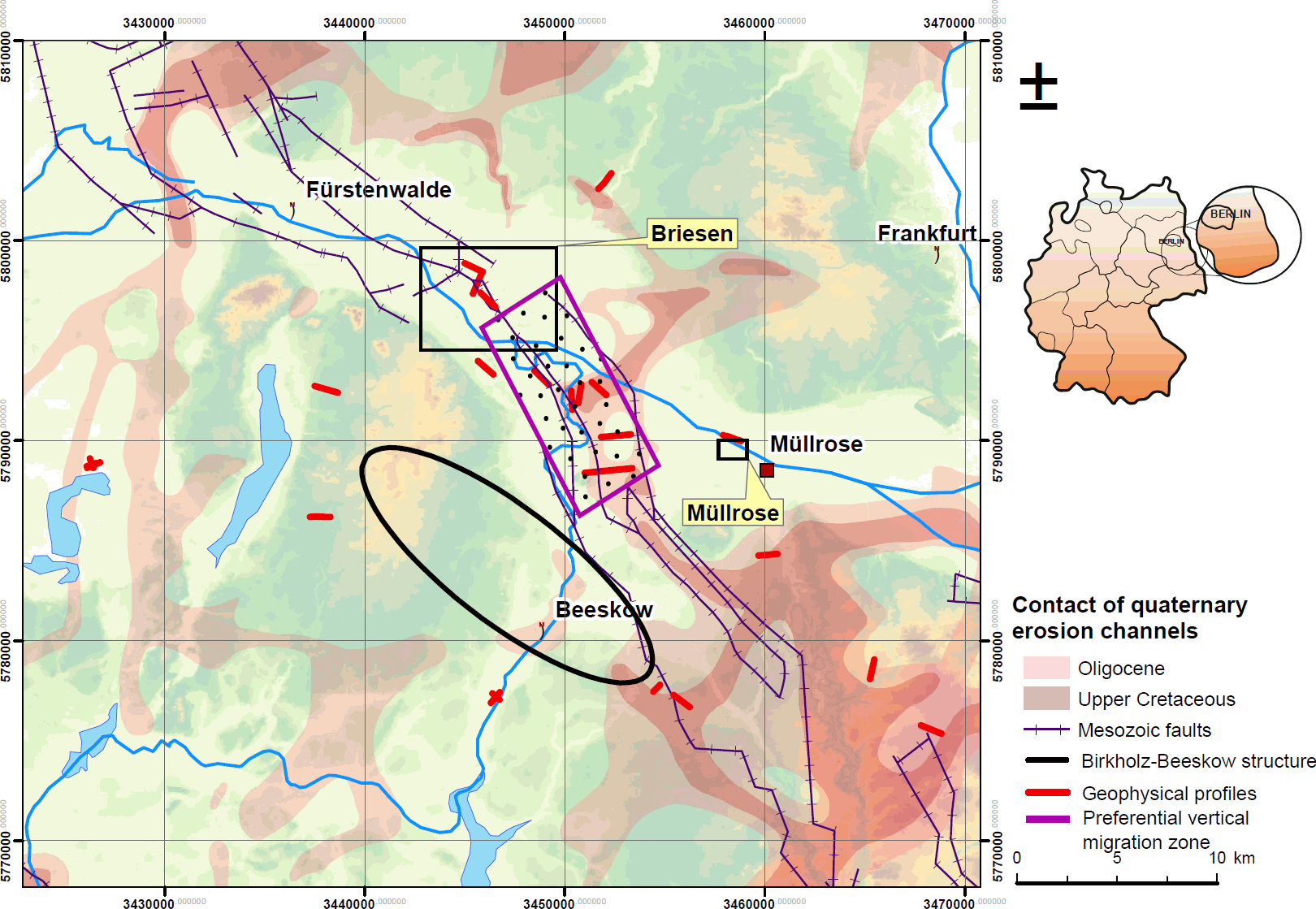
- stahlverrohrte Bohrlöcher als Elektroden (Günther u. a. 2015)
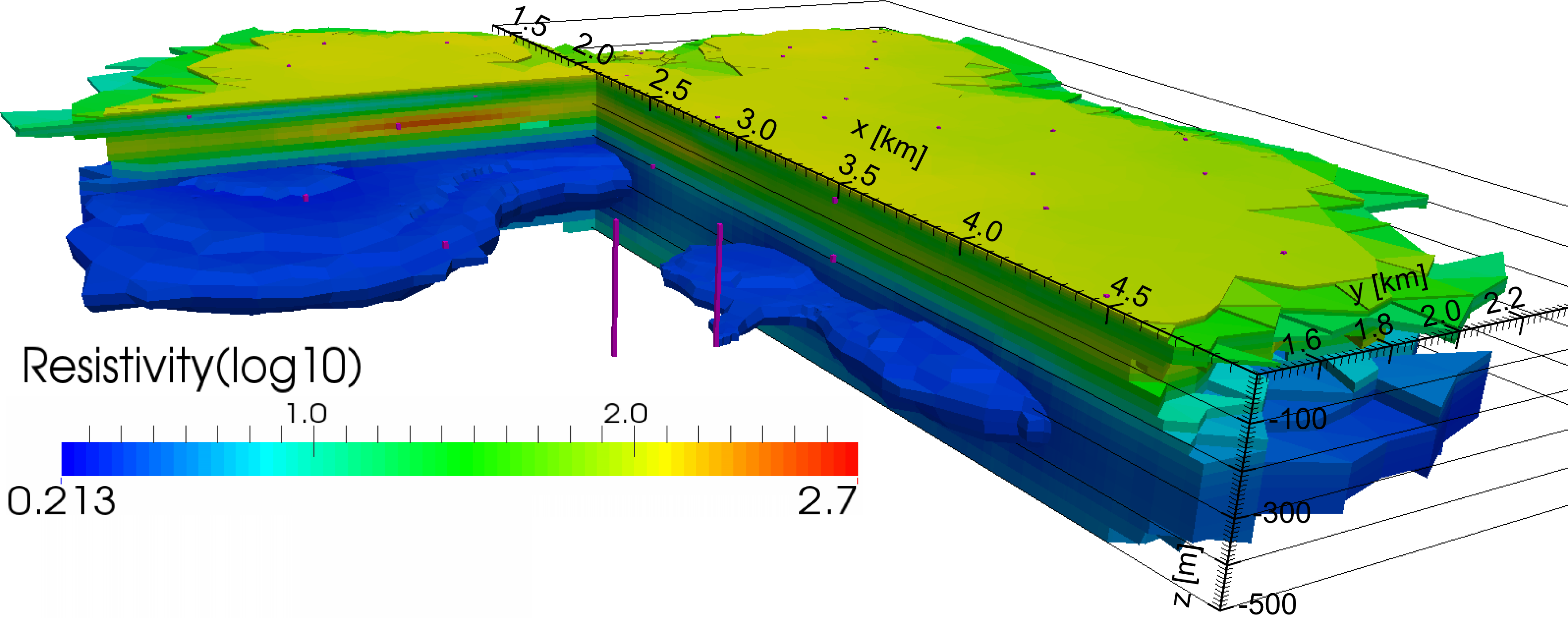
6.5.7 Ringelektroden
- Beispiel Salzwasser-Monitoring-System SAMOS