12 Magnetotellurik
- Natürliche Variationen des Magnetfeldes
- Messgrößen
- Aufbau einer MT-Station
- Daten-Processing
- Darstellungsgrößen
- Interpretation
- Grenzen
12.1 Einführung
Begriff: Magnetotellurik, lat. tellus, die Erde.
MT misst natürliche elektrische und magnetische Felder über einem breiten Frequenzspektrum.
Quelle der Felder: (a) Durch Sonnenwind und/oder EM-Strahlung erzeugte Ströme in Ionosphäre und Magnetosphäre mit \(0.01 < T < 10^4\) s, (b) weltweite Gewitteraktivität mit \(f < 10\) kHz
Klassische Arbeiten:
- A. N. Tikhonov (1950): On determining electrical characteristics of the deep layers of the earth’s crust, Dokl. Akad. Nauk S.S.S.R. 73, 295
- L. Cagniard (1953): Basic theory of the magneto–telluric method of geophysical prospecting, Geophysics, 18, 605-635
12.2 Anregungsspektrum
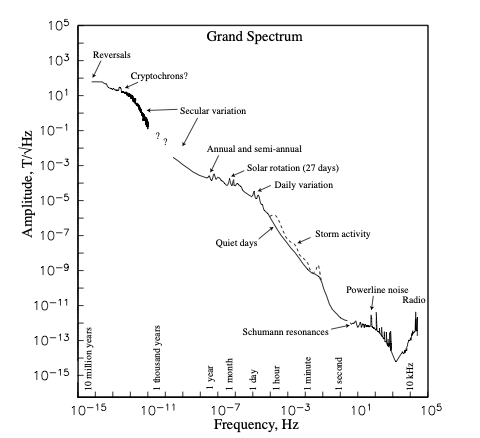
12.3 Daten
Registriert werden Felder als Zeitreihen \(\mathbf{E}(t), \mathbf{B}(t), \frac{ \partial \mathbf{B} }{ \partial t }(t)\)
Datenprocessing transformiert die registrierten Zeitreihen in den Frequenzbereich
Ziel: Bestimmung der Impedanz. Daraus werden Darstellungsgrößen wie Sondierungskurven des scheinbaren spezifischen Widerstandes usw. gewonnen
12.4 Theoretische Grundlagen
Aus dem System der Maxwellgleichungen erhalten wir die Helmholtz-Gleichung.
Eliminieren einer Feldgröße liefert PDE zweiter Ordnung \[ \curl \curl \vb{E} + i \omega \mu \sigma \vb{E} + \omega^{2} \mu \varepsilon \vb{E} = \vb{0} \] Bei niedrigen Frequenzen kann Verschiebungsstromdichte vernachlässigt werden: \[ \curl \curl \vb{E} + i \omega \mu \sigma \vb{E} = \vb{0} \] Mit Vektorindentität \[ \curl \curl \vb{f} = -\grad^{2} \vb{f} + \grad \divergence \vb{f} \] folgt Helmholtzgleichung \[ -\grad^{2}\vb{E} + i \omega \mu \sigma \vb{E} = \vb{0} \] oder, mit komplexer Ausbreitungskonstante \(k^{2}=-i \omega \mu_{0} \sigma\), \[ \grad^{2}\vb{E} + k^{2} \vb{E} = \vb{0}. \]
Quellen der MT sind Magnetfelder von Strömen in der Ionosphäre und Magnetosphäre. Wegen der großen Entfernung zur Quelle können diese Felder an der Erdoberfläche als ebene Welle mit vertikaler Ausbreitungsrichtung angenommen werden.
Wir nehmen o.B.d.A. weiterhin an, dass das magnetische Quellenfeld außerhalb der Erde ein in \(y\)-Richtung linear polarisiertes homogenes Feld ist: \[ \vb{H} = \begin{pmatrix} 0 \\ H_{y} \\ 0 \end{pmatrix} \] Das anregende Feld ist eine Transversalwelle mit \(\vb{H} \perp \vb{E} \perp \vb{k}\). Die Größe \(\vb{k}\) bezeichnet den Wellenvektor, welcher in Ausbreitungsrichtung zeigt. Zum anregenden Magnetfeld passt also \[ \vb{E} = \begin{pmatrix} E_{x} \\ 0 \\ 0 \end{pmatrix} \] Wie breiten sich die Felder \(\vb{E}\) und \(\vb{H}\) innerhalb der Erde aus? Da die anregenden Felder horizontal homogen sind, muss das auch für die Felder innerhalb der Erde (für \(z\geq 0\)) gelten.
Wir fragen also nach \(E_{x}(z)\).
Die Gleichung \[ \frac{ \partial^{2} E_{x} }{ \partial z^{2} } + k^{2} E_{x} = 0 \] hat in \(z\geq 0\) folgende Lösung: \[ E_{x}(z) = E_{x}(0) e^{ - i k z } \] Unter Beachtung des Vorzeichens von \(k = \pm \sqrt{ k^{2} }\) ergibt sich eine in pos. \(z\)-Richtung gedämpfte Welle.
Welches Vorzeichen muss für \(k\) gewählt werden?
Ansatz \(k^{2}= (\alpha - i \beta)^{2}\), daraus \[ k^{2} = \alpha^{2} - 2 i \alpha \beta - \beta^{2} = -i \omega \mu \sigma \] und \[ \alpha^{2} = \beta^{2} \] sowie \[ 2 \alpha \beta = \omega \mu \sigma \]
Schließlich \[ \alpha = \beta = \pm \sqrt{ \frac{\omega \mu \sigma}{2} } \] Damit \(E_{x}(z) \to 0\) für \(z \to \infty\), muss \(\beta > 0\) sein.
Wir zerlegen den Exponenten: \[ e^{ - i k z } = e^{ -i (\alpha - i \beta) z} = \underbrace{ e^{ - i \alpha z } }_{ \text{Welle} } \cdot\underbrace{ e^{ - \beta z } }_{ \text{Dämpfung} } \] Die Tiefe, in der die Amplitude der Welle auf den \(e\)-ten Teil der Oberflächenamplitude abgeklungen ist, wird Skintiefe oder elektromagnetische Eindringtiefe \(\tau\) genannt.
\[ \left|\frac{E_{x}(\tau)}{E_{x}(0)}\right| = e^{ -1 } = e^{ -\beta \tau } \] \[ \tau = \sqrt{ \frac{2}{\omega \mu \sigma} } \] Vereinfacht für Periodendauer \(T\) und spezifischen Widerstand \(\rho\) \[ \tau \approx 503 \sqrt{ \rho T } \] liefert Skintiefe in Metern.
Folgender Zusammenhang besteht zwischen elektromagnetischer Eindringtiefe und der Wellenlänge:
\[ \tau = \frac{\lambda}{2 \pi} \]
| Tiefe \(z=\) | Amplitude |
|---|---|
| \(\tau = \frac{\lambda}{2 \pi}\) | \(\| E_{x}(0)e^{ -1 }\| \approx 0.368 \| E_{x}(0)\|\) |
| \(\pi \tau = \frac{\lambda}{2}\) | \(\| E_{x}(0)e^{ -\pi }\| \approx 0.043 \|E_{x}(0)\|\) |
| \(2 \pi \tau = \lambda\) | \(\| E_{x}(0)e^{ -2\pi }\| \approx 0.002 \|E_{x}(0)\|\) |
12.5 Impedanz
Impedanz: Frequenzabhängiger Wellenwiderstand, \(Z(\omega)\).
Messgrößen: \(\vb{E}(\omega, \vb{r})\) und \(\vb{B}(\omega, \vb{r})\).
\[ Z(\omega) = \frac{\vb{e}_{h}\cdot \vb{E}}{(\vb{e}_{h} \times \vb{e}_{z})\cdot\vb{B}} \]
mit \(\vb{e}_{h}\): horizontaler kartesischer Einheitsvektor
Wir bezeichnen \[ Z_{s}(\omega) = \frac{E_{x}}{B_{y}} = -\frac{E_{y}}{B_{x}} \] als Oberflächenimpedanz.
Wie bekommen wir aus den Messgrößen \(\mathbf{E}\) und \(\mathbf{B}\) Informationen über die Leitfähigkeit des Untergrundes?
Beide Feldgrößen sind über die Maxwellgleichungen verknüpft. \[ \nabla \times \vb{E} = -i \omega \vb{B} \] Das Magnetfeld besitzt nur eine \(y\)-Komponente, also muss gelten \[ \frac{ \partial E_{x} }{ \partial z } - \underbrace{ \frac{ \partial E_{z} }{ \partial x } }_{ =0 } = -i \omega B_{y} \] woraus folgt: \[ B_{y}(z) = -\frac{1}{i \omega } \frac{ \partial E_{y}(z) }{ \partial z } = -\frac{1}{i \omega } \frac{ \partial }{ \partial z } E_{x}(0) e^{ - i k z } = \frac{k}{\omega } E_{x}(z) \]
In \(z=0\) \[ Z_{s} = \frac{E_{x}(0)}{B_{y}(0)} = \frac{\omega}{k} = Z_{1} \] Die Oberflächenimpedanz des homogenen Halbraums \(Z_{s}\) stimmt mit der intrinsischen Impedanz des homogenen Halbraums \(Z_{1}\) überein.
12.6 Darstellungsgrößen
Aus der Impedanz \(\mathbf{Z}_{s}\) werden der scheinbare spezifische Widerstand \(\rho_{s}\) sowie die Phase \(\Phi\) ermittelt und als Sondierungskurve dargestellt.
Definitionen:
\[ \begin{align} \rho_{s} & = \frac{1}{\omega \mu} |Z_{s}|^{2} \\ \Phi & = \arctan \frac{\text{Im}(Z_{s})}{\text{Re}(Z_{s})} \end{align} \]
Wie wir später sehen werden, beträgt der Phasenwinkel auf der Oberfläche eines homogenen Halbraums \(\Phi = \frac{\pi}{4}\), der scheinbare spezifische Widerstand stimmt mit spezifischen Widerstand des Halbraums überein.
12.7 Datenprocessing
Die Messwerte der MT liegen als Zeitreihen \(\mathbf{e}(t)\) und \(\mathbf{b}(t)\) vor.
Die MT-Station registriert
- Komponenten des E-Feldes \(E_x(t), E_y(t)\)
- Komponenten des H-Feldes \(H_x(t), H_y(t), H_{z}(t)\)
Die fundamentale Annahme der MT besteht darin, dass es einen linearen Zusammenhang zwischen den Horizontalkomponenten des E- und H-Feldes gibt.
Das Ziel des MT-Datenprocessings besteht in der Berechnung (genauer: Schätzung) des Impedanztensors \(\mathbf{Z}(\omega)\).
\[ \begin{pmatrix} E_x(\omega) \\ E_y(\omega) \end{pmatrix} = \begin{pmatrix} Z_{xx}(\omega) & Z_{xy}(\omega) \\ Z_{yx}(\omega) & Z_{yy}(\omega) \end{pmatrix} \begin{pmatrix} H_x(\omega) \\ H_y(\omega) \end{pmatrix}. \]
Das Processing der MT-Zeitreihen besteht grob aus folgenden Schritten:
- Instrumentenkorrekturen
- Berücksichtigung von Dipolauslage und Messkoordinatensystem
- Kenntnis des Frequenzganges der Sensorik
- Qualitätskontrolle: Sichtung und Rauschunterdrückung
- Entfernen von Spikes, Dropouts
- Beseitigen von gestörten Zeitreihenintervallen
- Aufteilen in Fenster
- überlappende Segmente der Länge \(T\)
- Taperung
- Fouriertransformation
- \(\hat{E}_i^{(k)}(\omega), \quad \hat{H}_j^{(k)}(\omega)\), \(i,j \in {x,y}\)
- komplexwertige Fourierkoeffizienten für diskrete Frequenzen
- Spektrale Schätzung
- Berechnung von Kreuz- und Autospektren für jede Frequenz
- Robuste lineare Regression für \(\mathbf{Z}\)
- Fehleranalyse
- Berechnung der Darstellungsgrößen
Das MT-Datenprocessing ist ein multivariates lineares Ausgleichsproblem im Frequenzbereich.