4 Sensitivitäten und Messanordnungen
4.1 Herleitung
Gegeben sei eine Vier-Punkt-Anordnung AB-MN, bei einer Leitfähigkeitsverteilung \(\sigma\) ergibt sich eine Mess-Spannung \(\varphi_{MN}\) bei einem Einspeisestrom \(I_{AB}\). Frage: Wie wirkt sich eine Änderung der Leitfähigkeit \(\delta\sigma\) auf den Messwert \(\varphi_{MN}+\delta\varphi_{MN}\) aus?

Dabei betrachten wir als Messgröße den scheinbaren spezifischen Widerstand \(\rho_a\) und als Variable den spezifischen Widerstand \(\rho\), um eine einheitenlose Größe zu erhalten.
\[S(\vb r)=\pdv{\rho_a}{\rho(\vb r)}\]
Diese wird als Sensitivitätsfunktion bezeichnet.
Wir setzen \(\sigma+\delta\sigma\) in die Kontinuitätsgleichung ein:
\[\div((\sigma+\delta\sigma)\grad (u+\delta u))=\]
\[\div(\sigma\grad u)+\div(\delta\sigma\grad u)+\div(\sigma\grad \delta u)+\div(\delta\sigma\grad \delta u)=I\delta(\vb r-\vb r_s)\]
Geselowitz (1971):
\[\Rightarrow S(\vb r)=\frac{k}{\rho^2} \int\Omega\frac{\grad u^{AB}}{I^{AB}} \frac{\grad u^{MN}}{I^{MN}}\dd\Omega\]
Im homogenen Halbraum können wir die Lösung einsetzen und erhalten
\[\Rightarrow S(\vb r)=\frac{k}{4\pi^2} \int_\Omega\qty(\frac{\vb r_A}{r_A^3}-\frac{\vb r_B}{r_B^3})\vdot\qty(\frac{\vb r_M}{r_M^3}-\frac{\vb r_N}{r_N^3})\dd\Omega\]
Im Folgenden betrachten wir ausschließlich die Sensitivität des homogenen Halbraums, was für das Verständnis völlig ausreichend ist. Natürlich hängt die Potentialverteilung von der Leitfähigkeit selbst ab. Insbesondere wenn man Logarithmen betrachtet, ist der Grad der Nichtlinearität aber klein, so dass die grundlegenden Bilder bei kleinen Kontrasten sehr ähnlich sind.
Man beachte außerdem, dass Strom- und Potential-Elektroden austauschbar sind. Wir diskretisieren den Untergrund in ein Dreiecksnetz und integrieren die Funktion über Gauss-Quadratur:
Die Wenner-Anordnung zeigt oberflächennah eine Abfolge von positiven und negativen Vorzeichen (Skala ist normiert). Eine Oberflächennahe Erhöhung (bis 1m Tiefe) würde ein zentrales Maximum mit zwei flankierenden Minima (und daran anschließend wieder Maxima) zeigen. Generell ist die Anordnung bis zu einer Tiefe sensitiv, die etwas kleiner als der Elektrodenabstand ist.
Die Funktion der Schlumberger-Anordnung ist generell ähnlich,
nur dass der mittlere Bereich schmaler ist. Anordnungen mit Spannungsmessung innerhalb der Stromelektroden werden als \(\alpha\)-Typ bezeichnet (die einfach Wenner-Anordnung auch Wenner-\(\alpha\) genannt). Wenn man Strom- und Spannungselektroden trennt, aber die Abstände gleich behält, erhält man die Wenner-\(\beta\) Anordnung
Bei der Dipol-Dipol-Anordnung werden die Spannungs- und Strom-Strecken nicht mit vergrößert und bleiben daher kleiner als der Dipol-Abstand.
4.2 Sensitivitäten erklärt
Die Frage erlaubt sich: Wie kommt es denn zur Verteilung der positiven und negativen Sensitivitäten? Kann man das plausibel erklären?
Wir betrachten die Potentialverteilung und Stromlinien einer Wenner-Messung (A-M-N-B) und wie sie sich verändern wenn Anomalien eingebracht werden, siehe dazu auch Slidedeck 2 zur Überblendung. Zunächst der homogene Fall:
Nun erzeugen wir kleine flache Einlagerungen (Kreise), zunächst im Bereich der negativen Sensitivitäten.
Während auf der rechten Seite wenige Änderungen zu verzeichnen sind, sehen wir, dass die Stromlinien die Einlagerung umgehen und die Potentiallinien nach links verschoben werden, also die Potentialdifferenz sinkt. Damit sinkt auch der scheinbare spezifische Widerstand aufgrund der Widerstands-Erhöhung, was einer negative Sensitivität entspricht.
Wenn wir die Einlagerung stattdessen leitfähig machen (Verringerung des spez. Widerstands), werden die Stromlinien hineingezogen und die Potentialdifferenz steigt.
Nun verschieben wir die Einlagerung in die Mitte, den Bereich der positiven Sensitivitätsverteilung, zunächst mit einem erhöhten Widerstand. Durch die Verschiebung der Stromlinien nach außen werden die Potentiallinien auf beiden Seiten nach innen gezogen, wodurch die Spannung steigt und damit der scheinbare spez. Widerstand. Dies entspricht einer positiven Sensitivität, die sich fast überall ergibt.
Wenn wir die zentrale Einlagerung leitfähig machen (Verringerund des spez. Widerstands), werden die Stromlinien hinein gezogen und die Potentiallinien nach außen geschoben, wodurch ihre Differenz (die Spannung) sinkt und damit der scheinbare spez. Widerstand.
4.3 Mess-Strategien
“Bewegung” einer festen Anordnung entlang eines Profils
Vergrößerung der Auslage bei festem Mittelpunkt
Kombination aus Kartierung und Sondierung, meist bei festem Aufbau einer Elektrodenkette (Multielektroden-Geoelektrik): Electrical Resistivity Tomography (ERT)
4.3.1 Widerstands-Kartierung
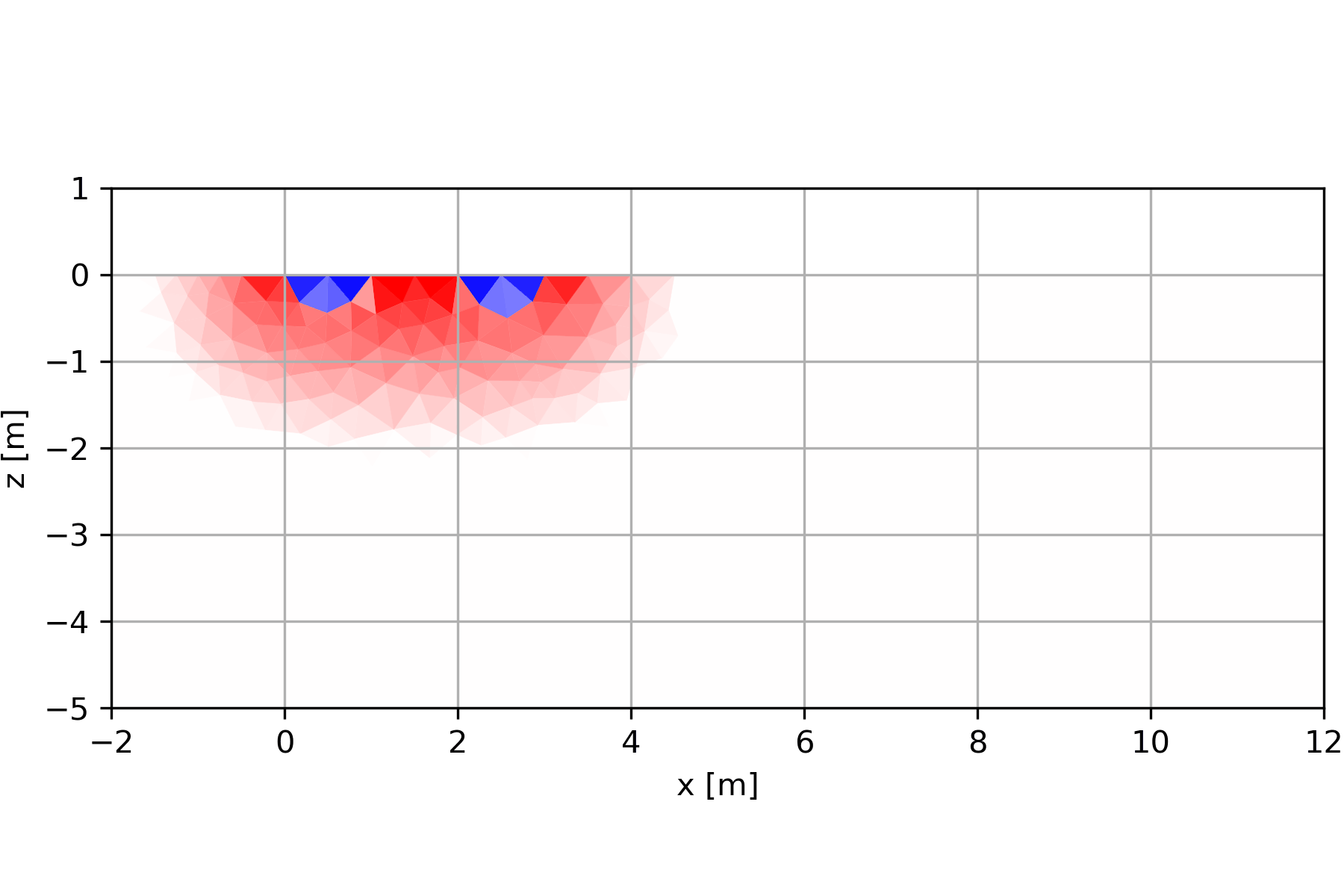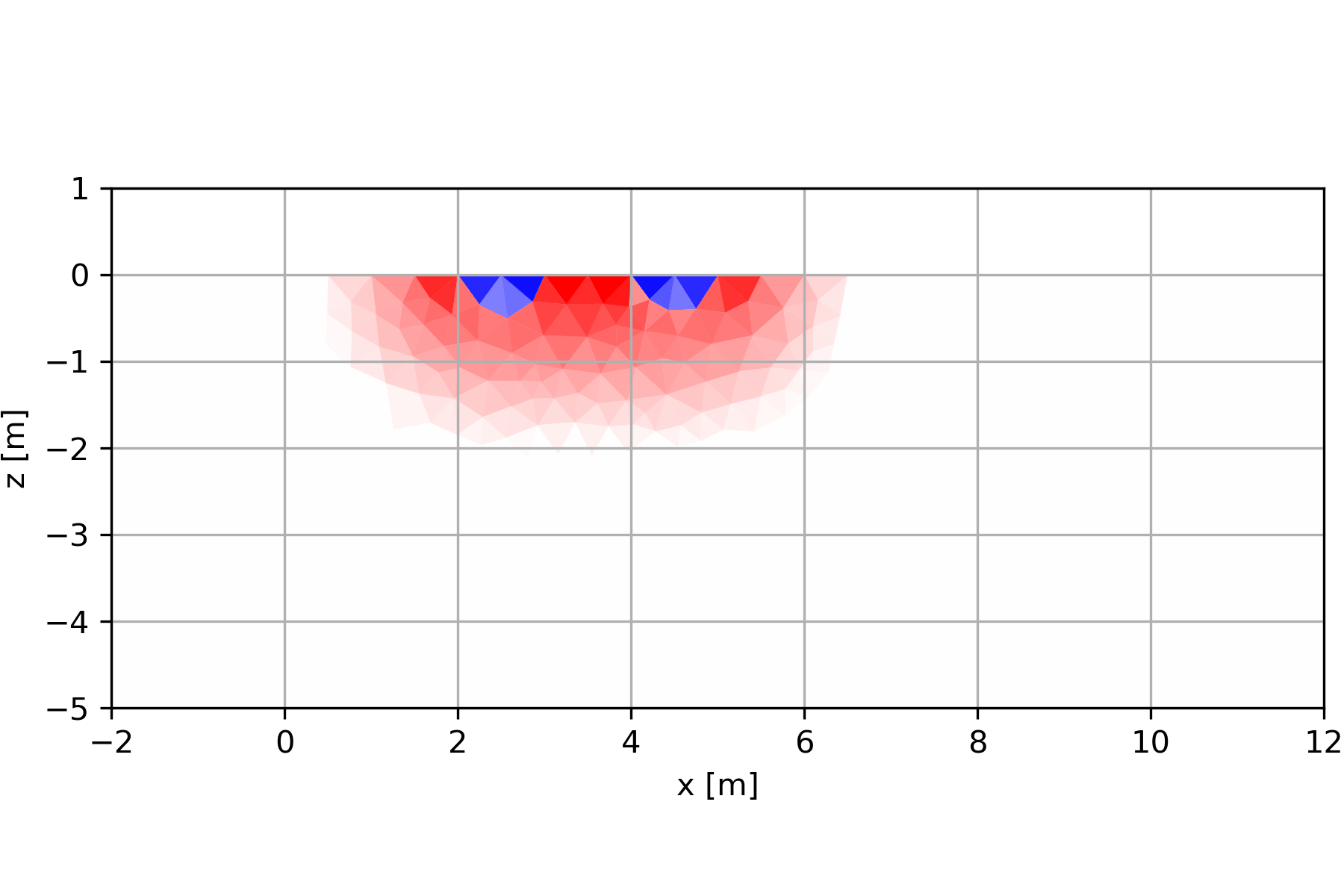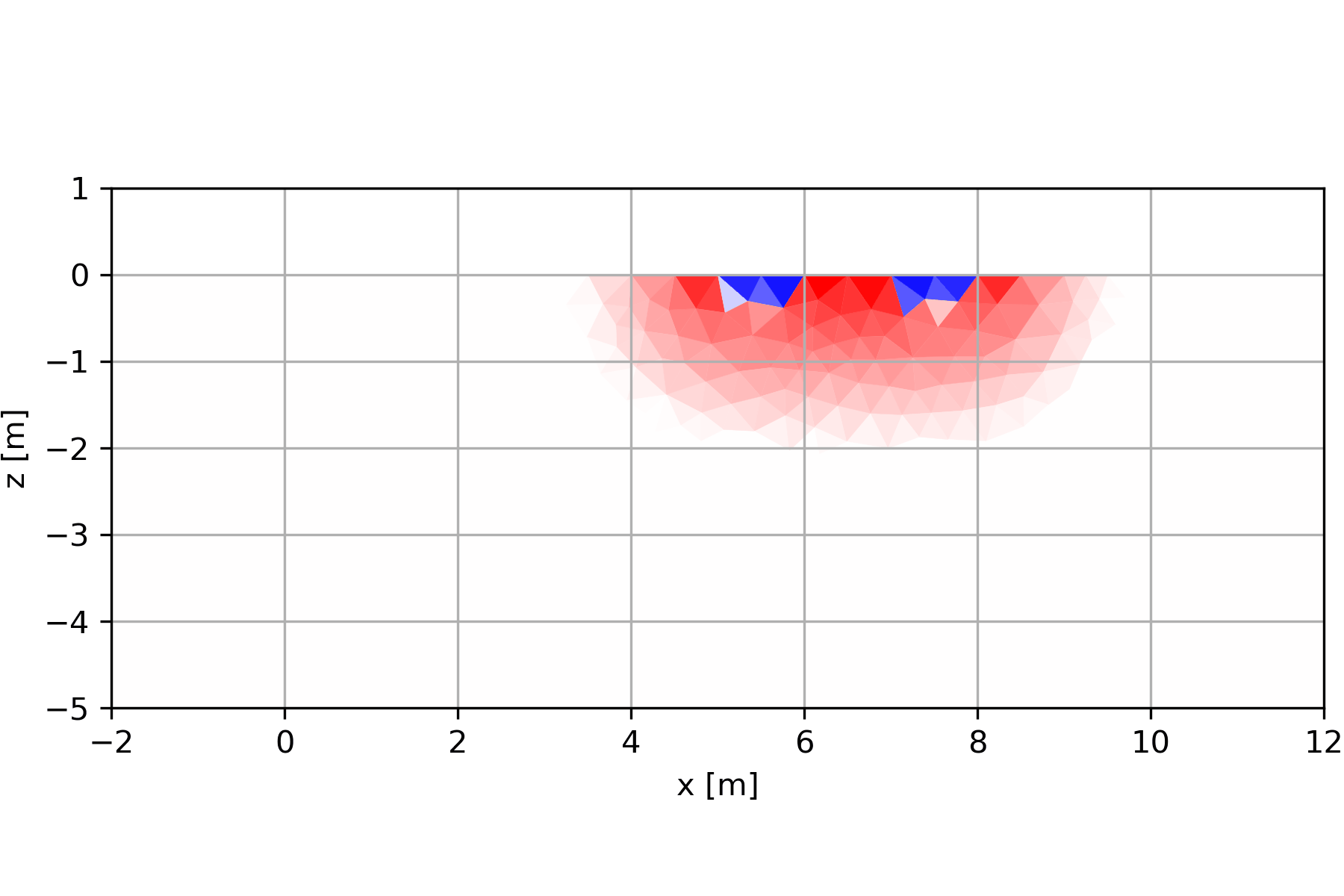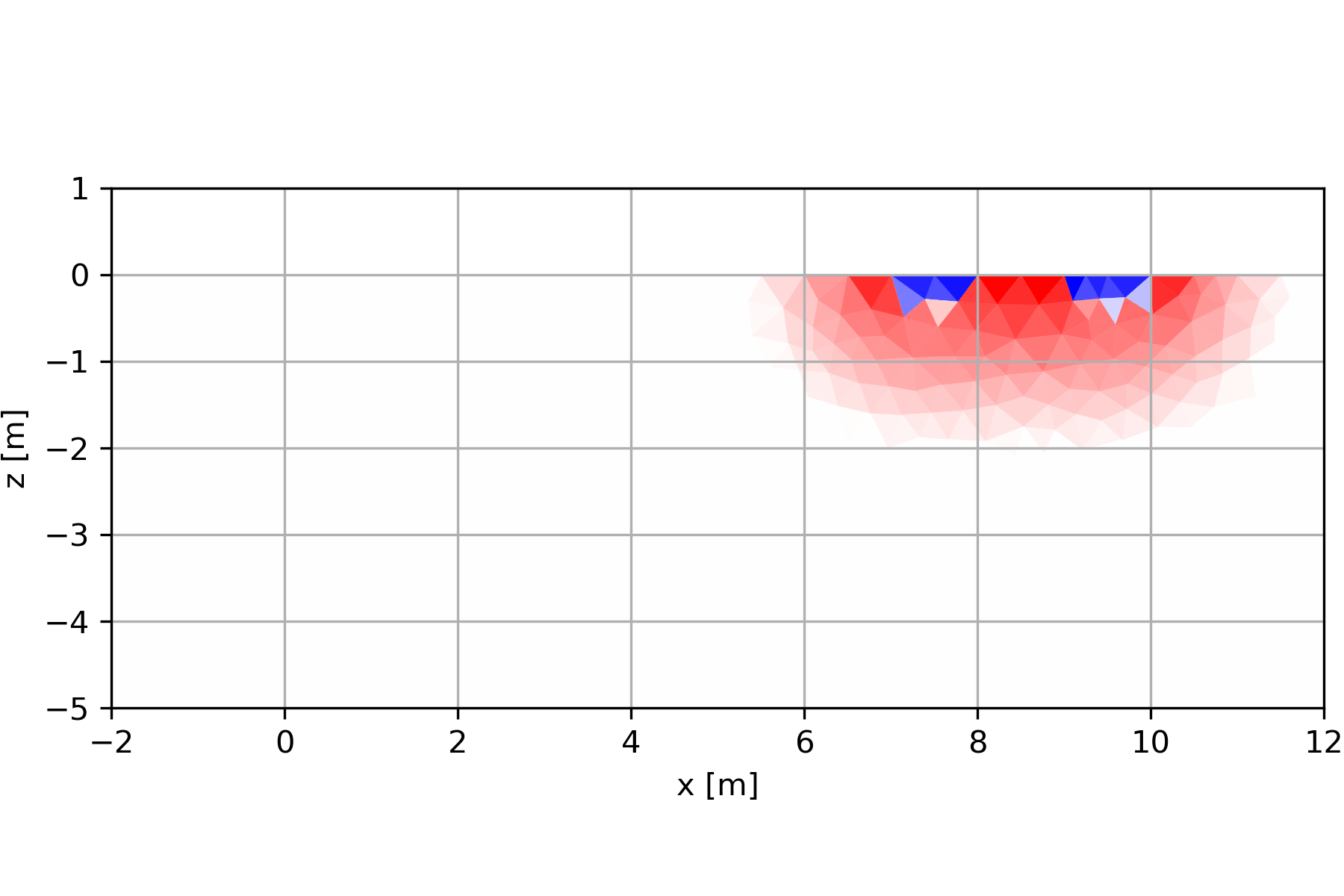
Kartierungen mit festen Anordnungen werden heutzutage nur noch selten eingesetzt (wenn die Teufenlage eines zu suchenden, eher kleineren Objekts gut bekannt ist). Auch Sondierungen, die zur Erkundung von horizontal geschichteten Untergründen eingesetzt werden) treten immer weiter in den Hintergrund. Bei weitem häufigstes Verfahren ist die 2D-Geoelektrik (nur noch selten als Sondierungs-Kartierung bezeichnet). Manchmal werden 3D-Anordnungen oder Anordnungen unter Zuhilfenahme von Bohrlöchern eingesetzt.