8  Induzierte Polarisation

8.1 Äquivalente Pumpen-Kreise

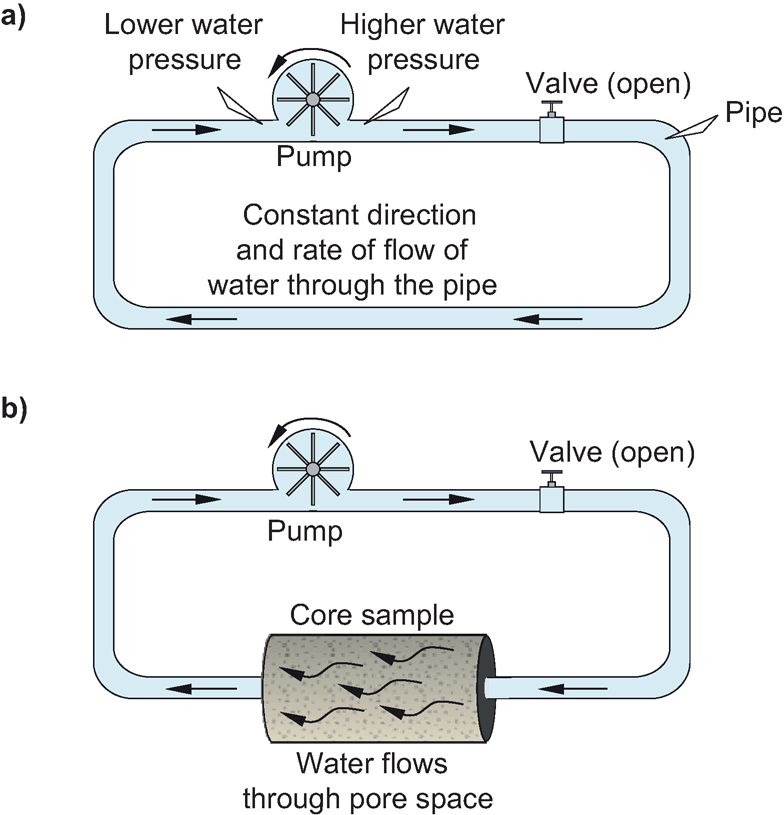
8.1.1 Gleichstrom-Äquivalent

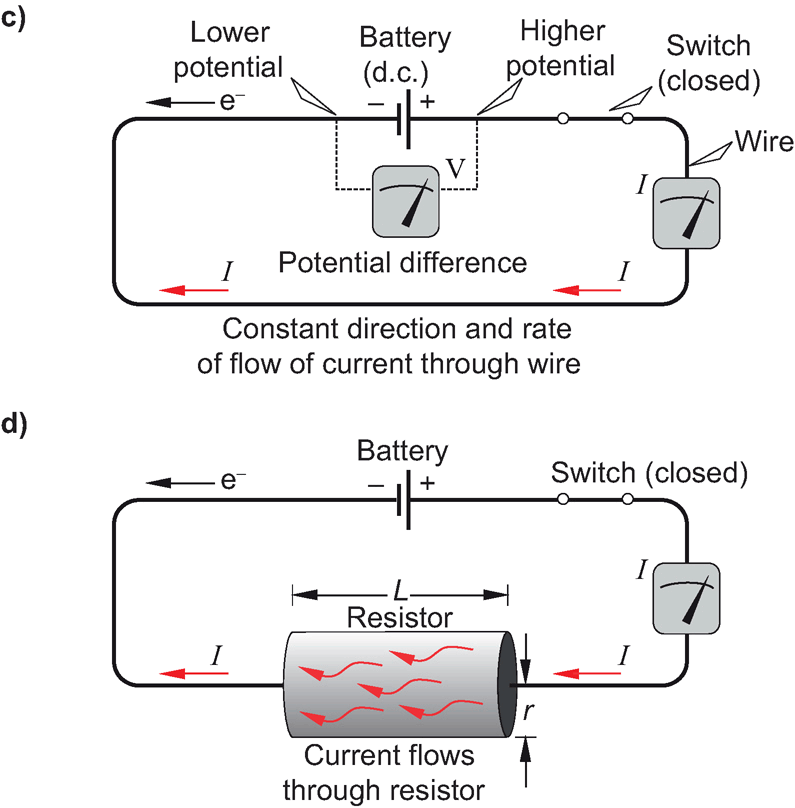
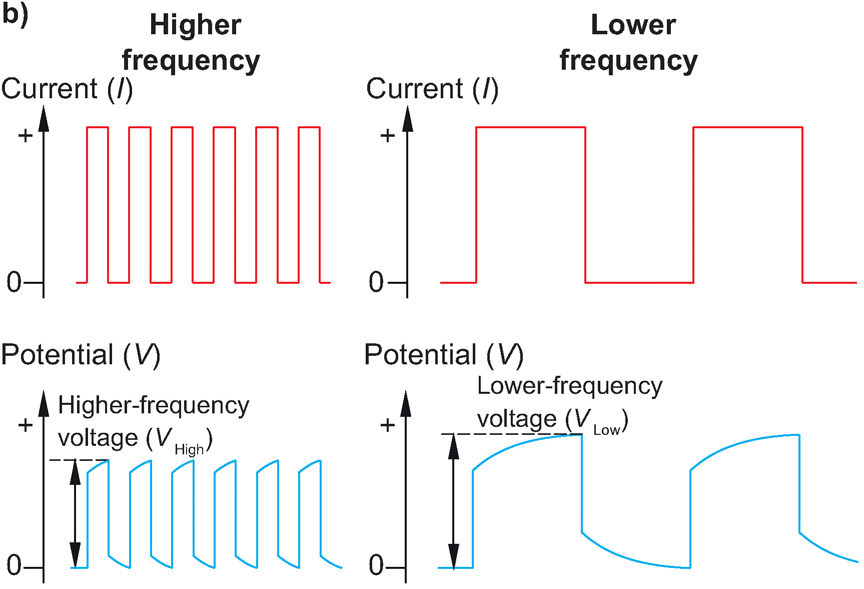
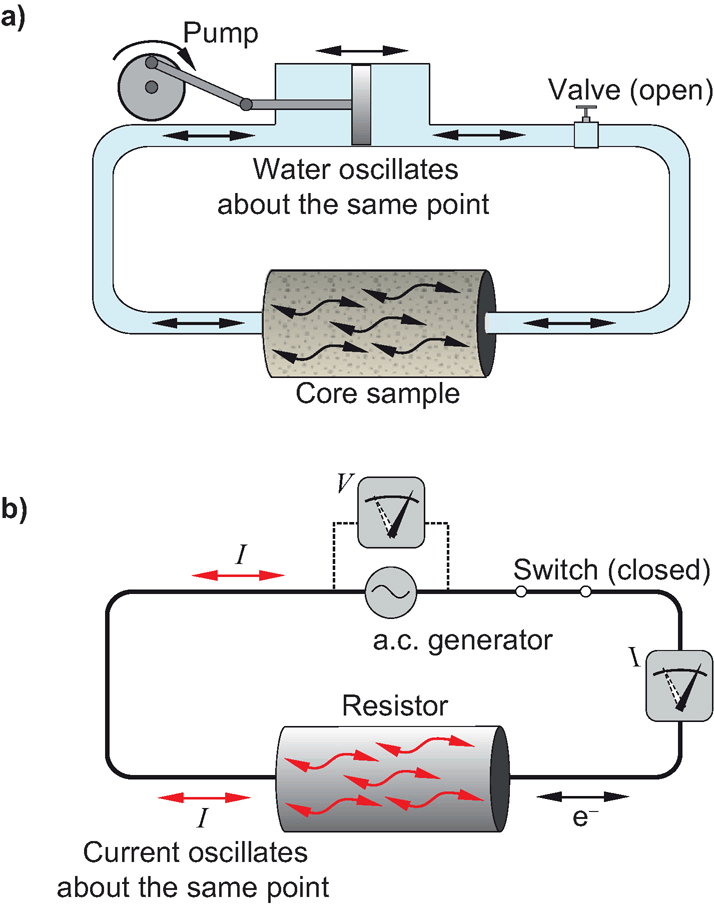
Pumpenkreislauf (Dentith und Mudge 2014, Fig. 5.3)

Stromkreislauf (Dentith und Mudge 2014), Fig. 5.3

8.1.2 Wechselstrom-Äquivalent (Dentith&Mudge)

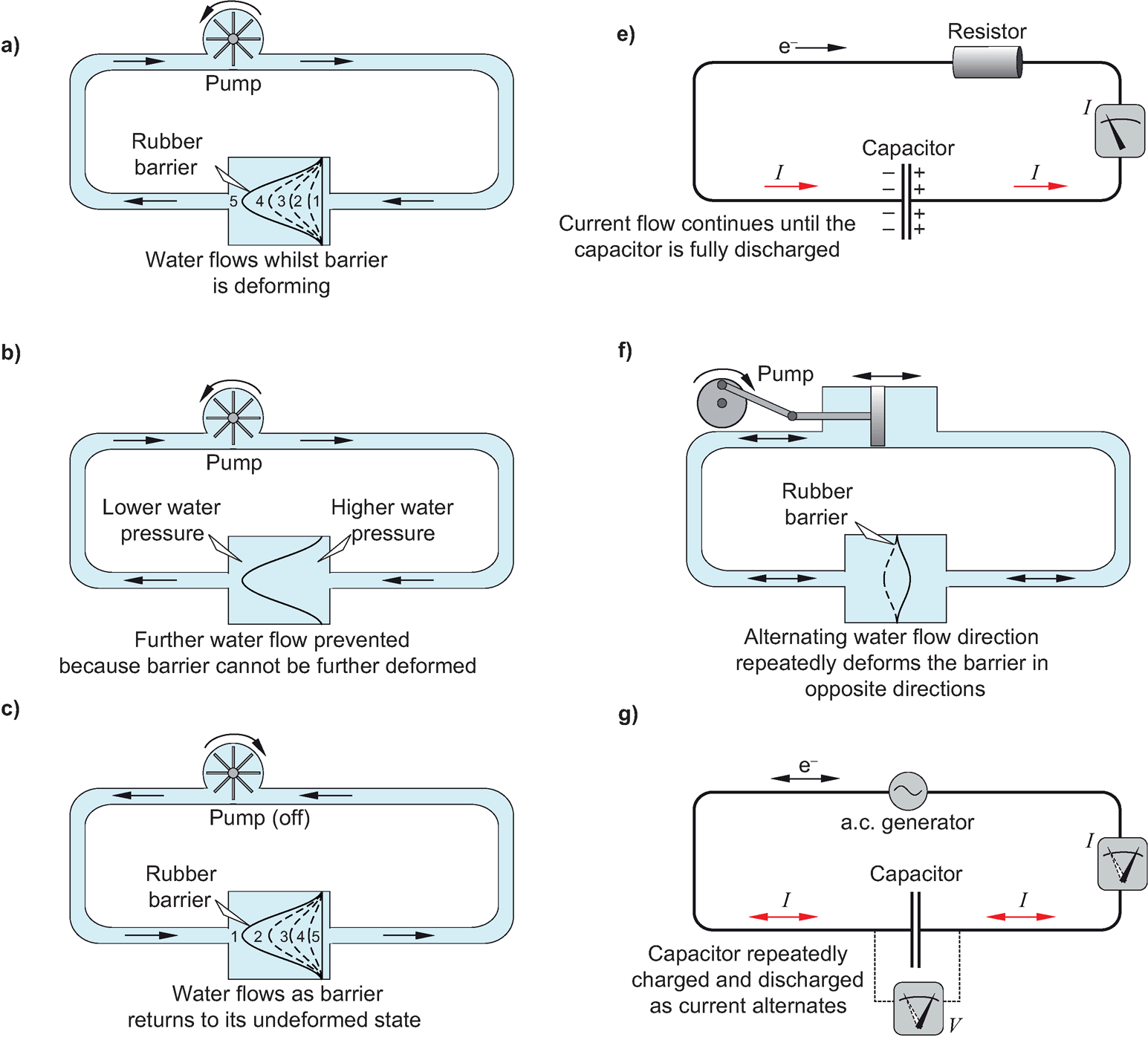
Resistor im Wechselstrom-Kreislauf (Dentith und Mudge 2014, Fig. 5.4)

Kapazität im Wechselstrom-Kreislauf (Dentith und Mudge 2014, Fig. 5.4)

8.2 Induzierte Polarisation - Zeitbereich

(Dentith und Mudge 2014)

8.3 Induzierte Polarisation - Frequenzbereich

(Dentith und Mudge 2014)

8.3.1 Phasenverschiebung

(Dentith und Mudge 2014)

\[ \sigma^* = \sigma' + \imath\sigma'' = |\sigma| e^{\imath\phi} \]

8.4 Induzierte Polarisation

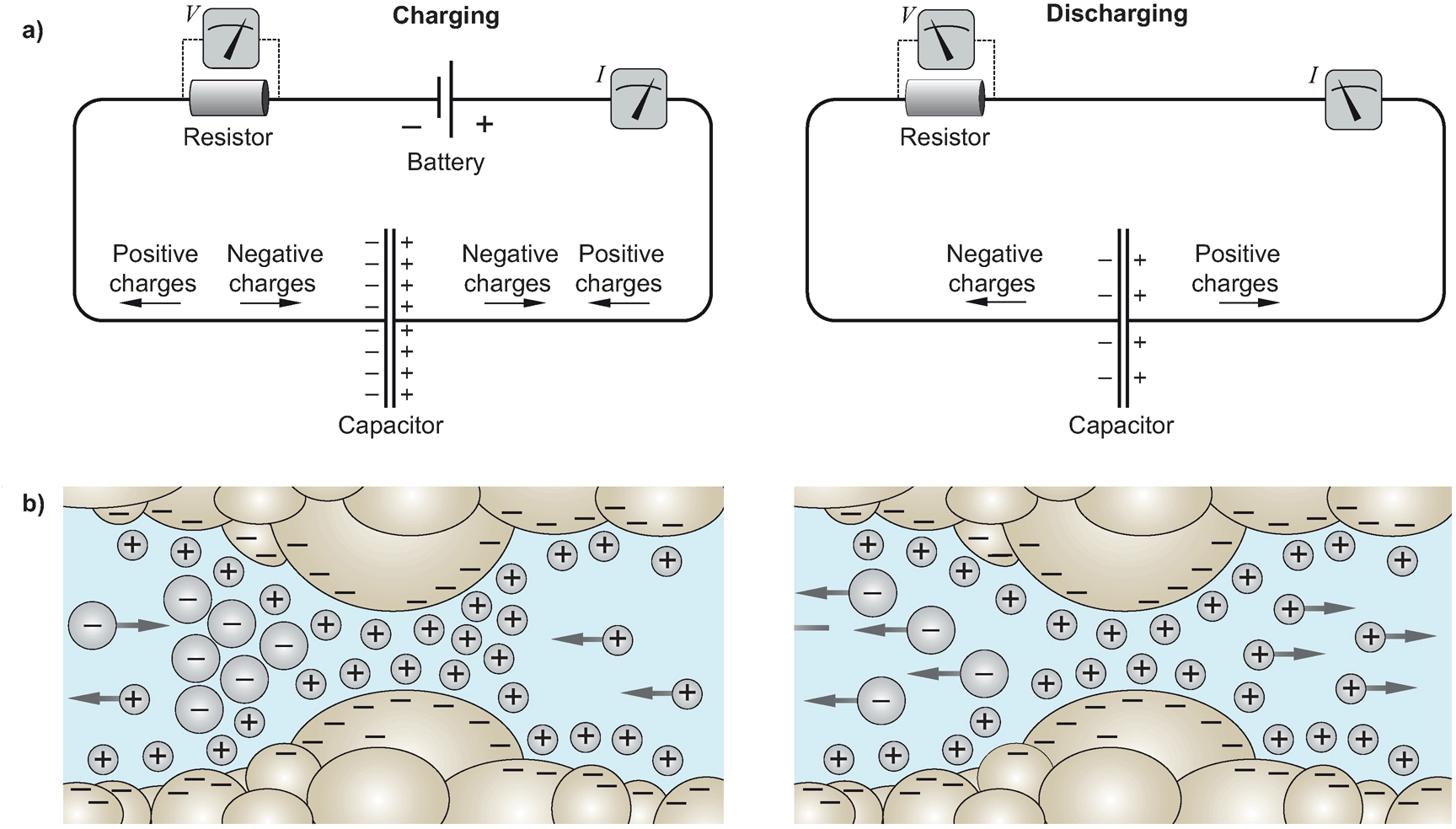
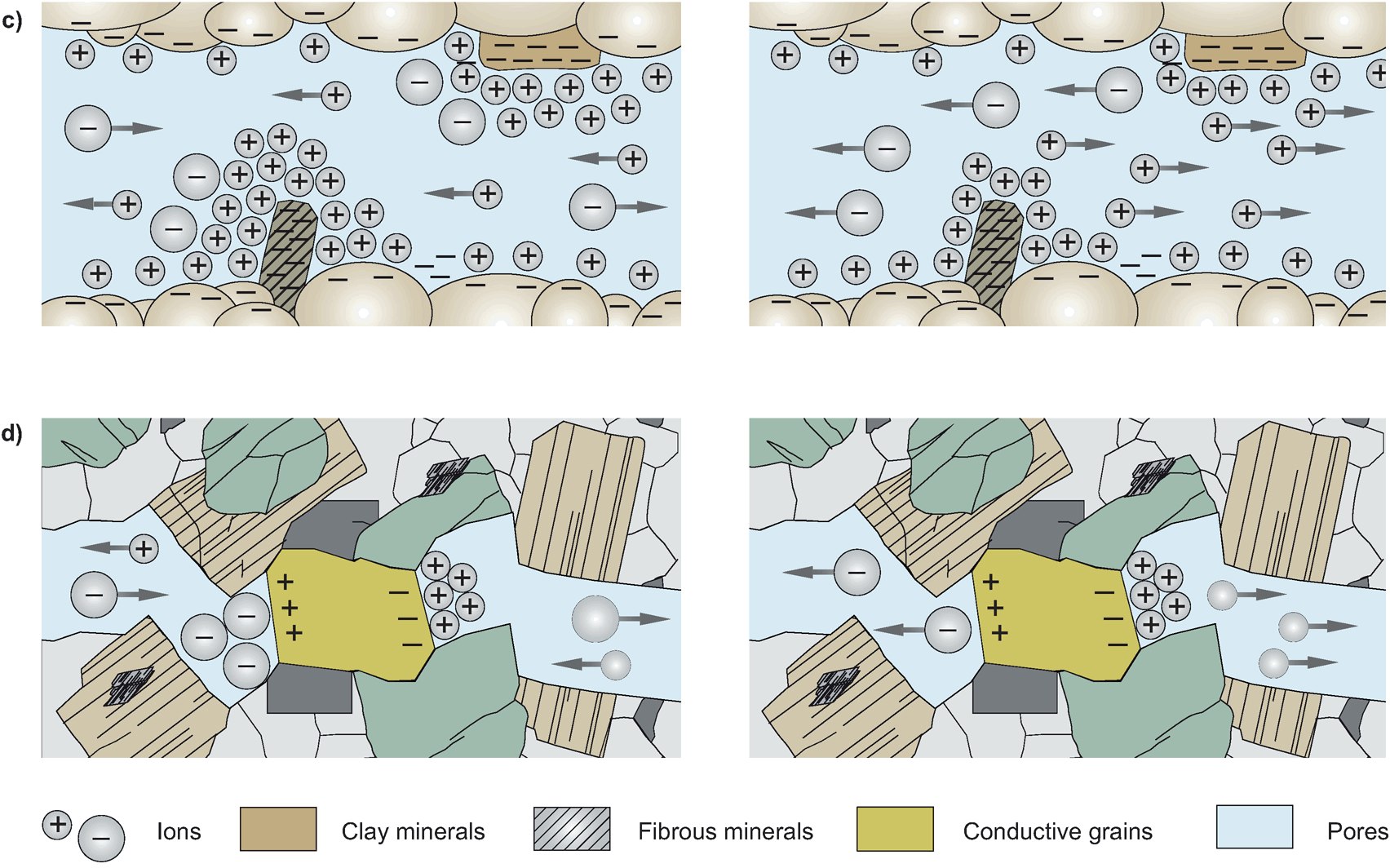
Polarisationsmechanismen (Dentith und Mudge 2014, Fig. 5.19)

8.5 Leitfähigkeit vs. Permittivität

\[ \vb j = \curl\vb H=\sigma\vb E+\epsilon\dot{\vb E}=\sigma\vb E + \imath\omega\vb E = (\sigma+\imath\omega)\vb E = (\frac{\sigma}{\imath\omega}+\epsilon)\dot{\vb E} \]

\[ \sigma^* = \sigma' + \imath\sigma'' = \sigma + \imath\omega\epsilon \]

\[ \rho^* = (\sigma^*)^{-1} = \frac{\sigma' - \imath\sigma''}{\sigma'^2 + \sigma''^2} = \frac{\sigma' - \imath\sigma''}{|\sigma^*|^2} = \rho' - \imath\rho'' = |\rho^*|e^{-\imath\phi} \]

8.6 Relaxationen

Relaxationen (Loewer u. a. 2017)

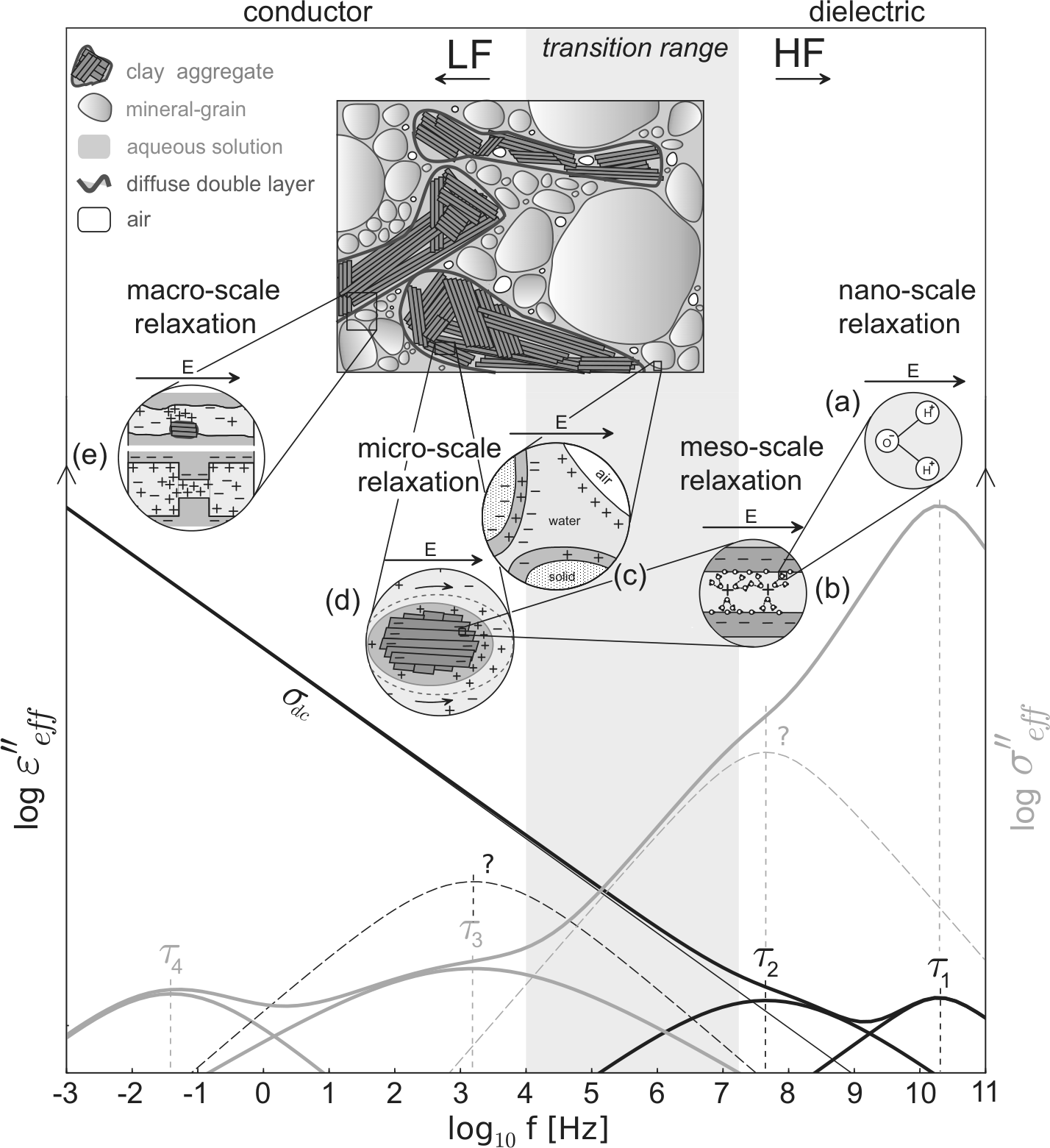
8.6.1 Debye-Relaxation

  • fundamentale Polarisation

\[ \sigma(\omega)=\sigma_\infty + (\sigma_0-\sigma_\infty)\frac{m}{\imath\omega\tau} \]

  • exponentielles Abklingen

\[ U(t) = U_0 m e^{-t/\tau} \]

8.7 Kramers-Kronig Beziehungen

Zusammenhang Real- und Imaginärteil analytischer Funktionen

\[ \rho''(\omega) = \frac{2\omega}{\pi}\int\limits_0^\infty \frac{\rho'(x)-\rho'(\omega)}{x^2-\omega^2}\dd x \]

\[ \rho'(\omega) = \rho'(\infty) + \frac{2}{\pi}\int\limits_0^\infty \frac{x \rho''(x)-\omega\rho''(\omega)}{x^2-\omega^2}\dd x \]

8.8 Kramers-Kronig Beziehungen

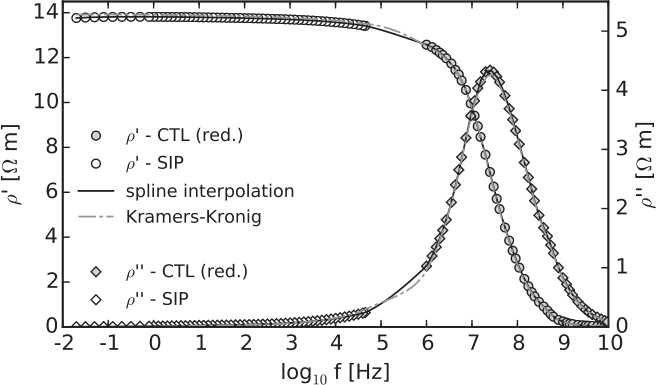
IP & DK Messung an Loess (Loewer u. a. 2017)

8.9 Spektrale Induzierte Polarisation (SIP)

REFERENCE

9 Feld-IP

  • Messung im Frequenzbereich
    • genau, nicht robust
  • Messung im Zeitbereich
    • klassische Multielektrode
  • Auswertung mit pyBERT
    • Klassen für FDIP und TDIP
    • Prozessing & Inversion

SIP256C im Gelände (Günther und Martin 2016)

9.1 Vergleich von Geräten (Martin et al., 2020)

SIP256C, MPT DAS-1, ABEM Terrameter LS2, Syscal Pro Switch 72 (Martin u. a. 2020)

Scheinbare spez. Widerstände (Martin u. a. 2020)

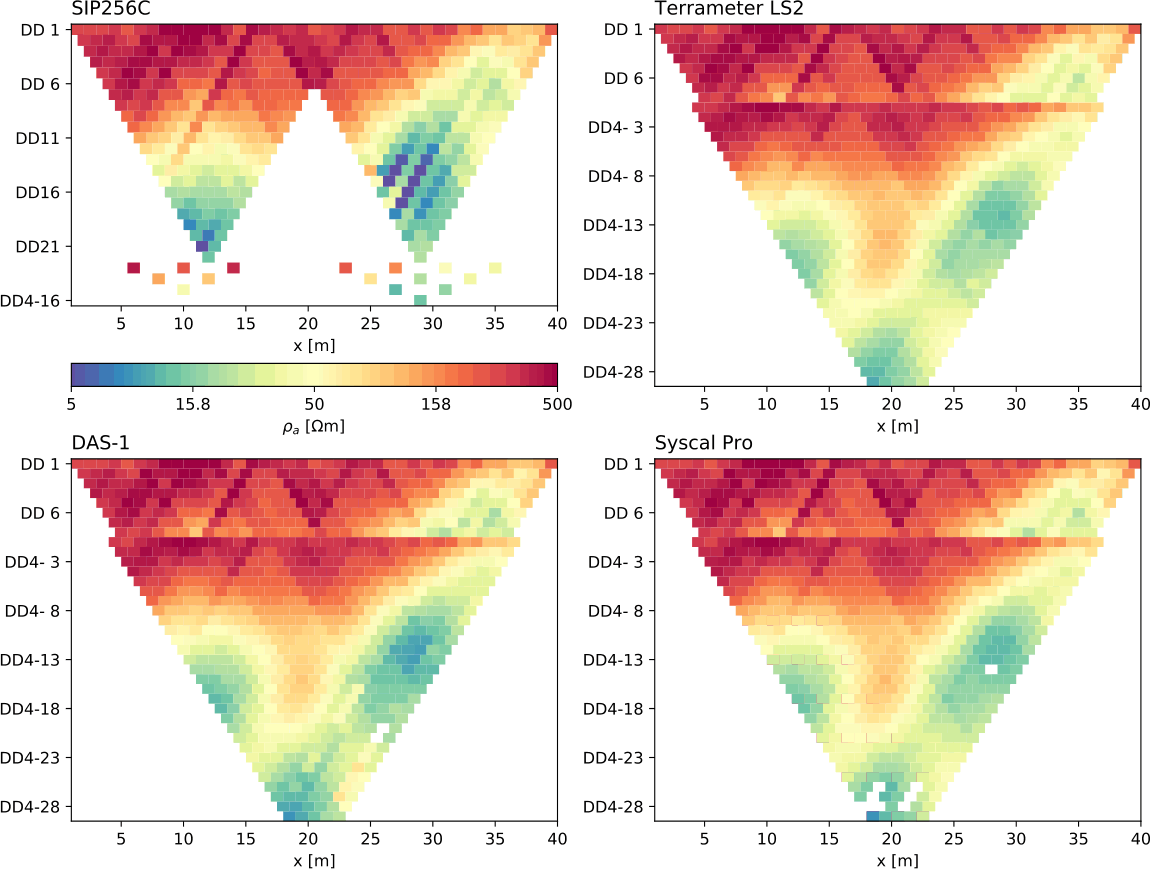
9.1.1 FDIP

FDIP - Phasen (Martin u. a. 2020)

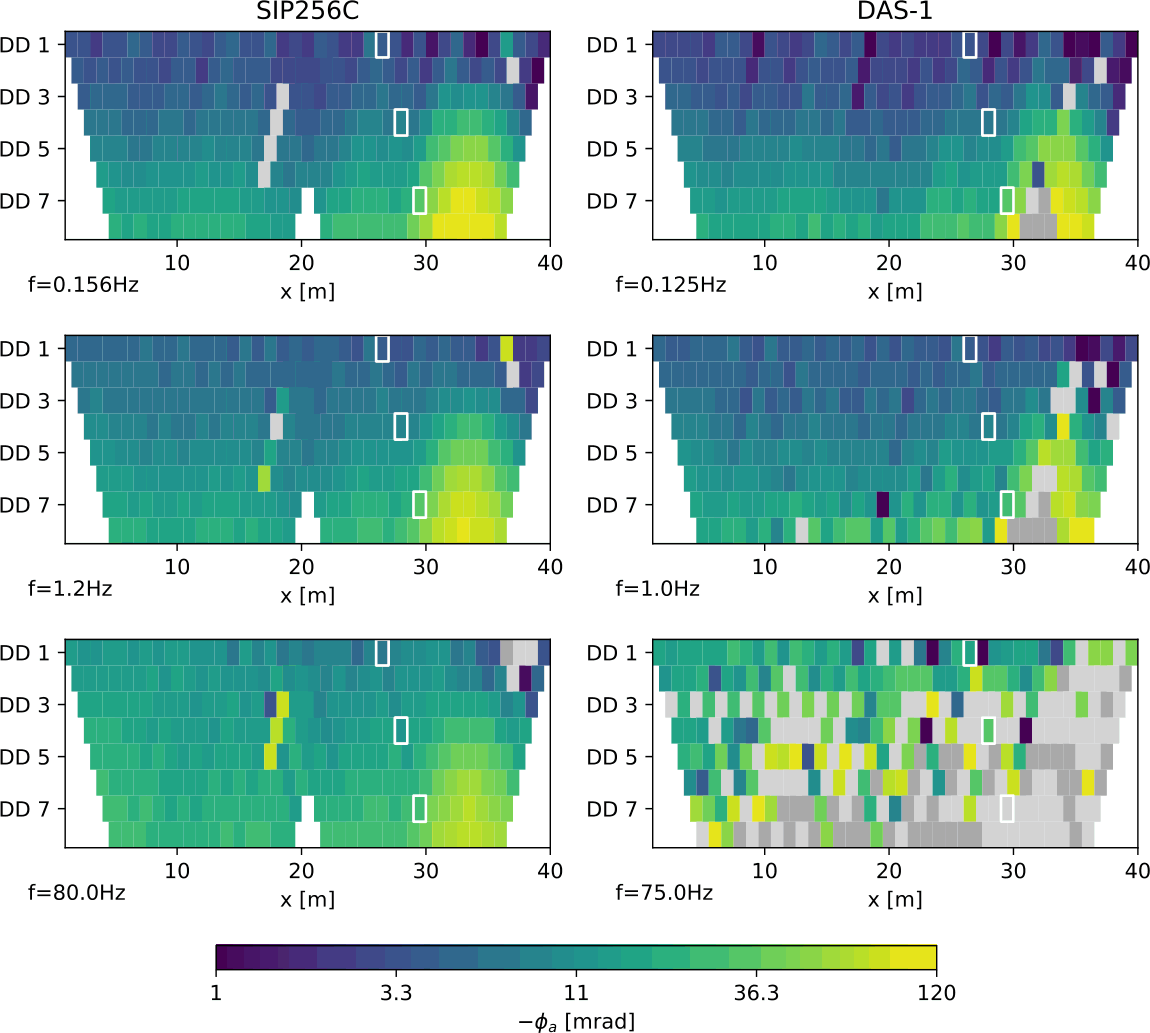
9.1.2 TDIP

TDIP-Zeitreihen (Martin u. a. 2020)
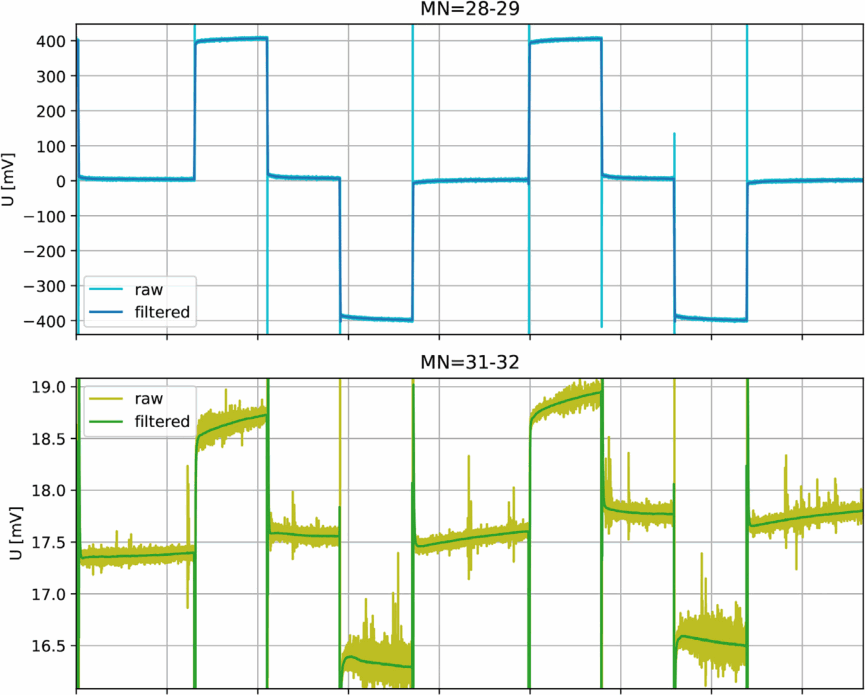
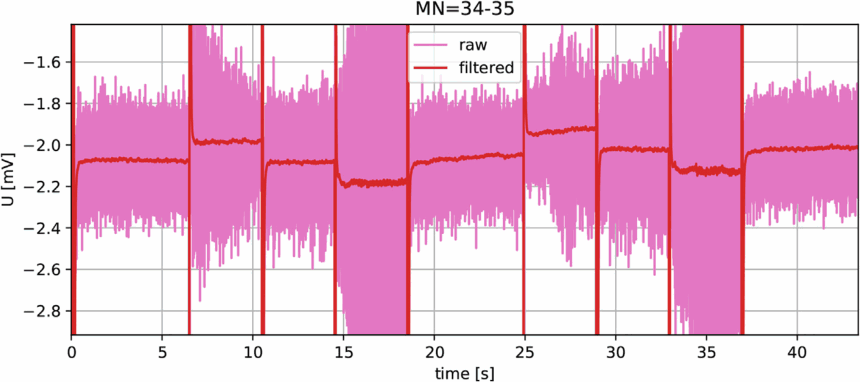
  • Filter: Tiefpass, 50Hz, Offset, Drift, Elektrodenpolarisation
  • Gating & Stapelung \(\Rightarrow\) Decay

TDIP - Gating (Martin u. a. 2020)

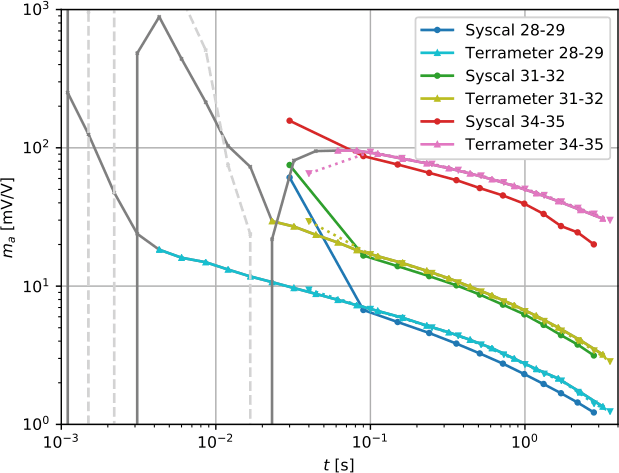
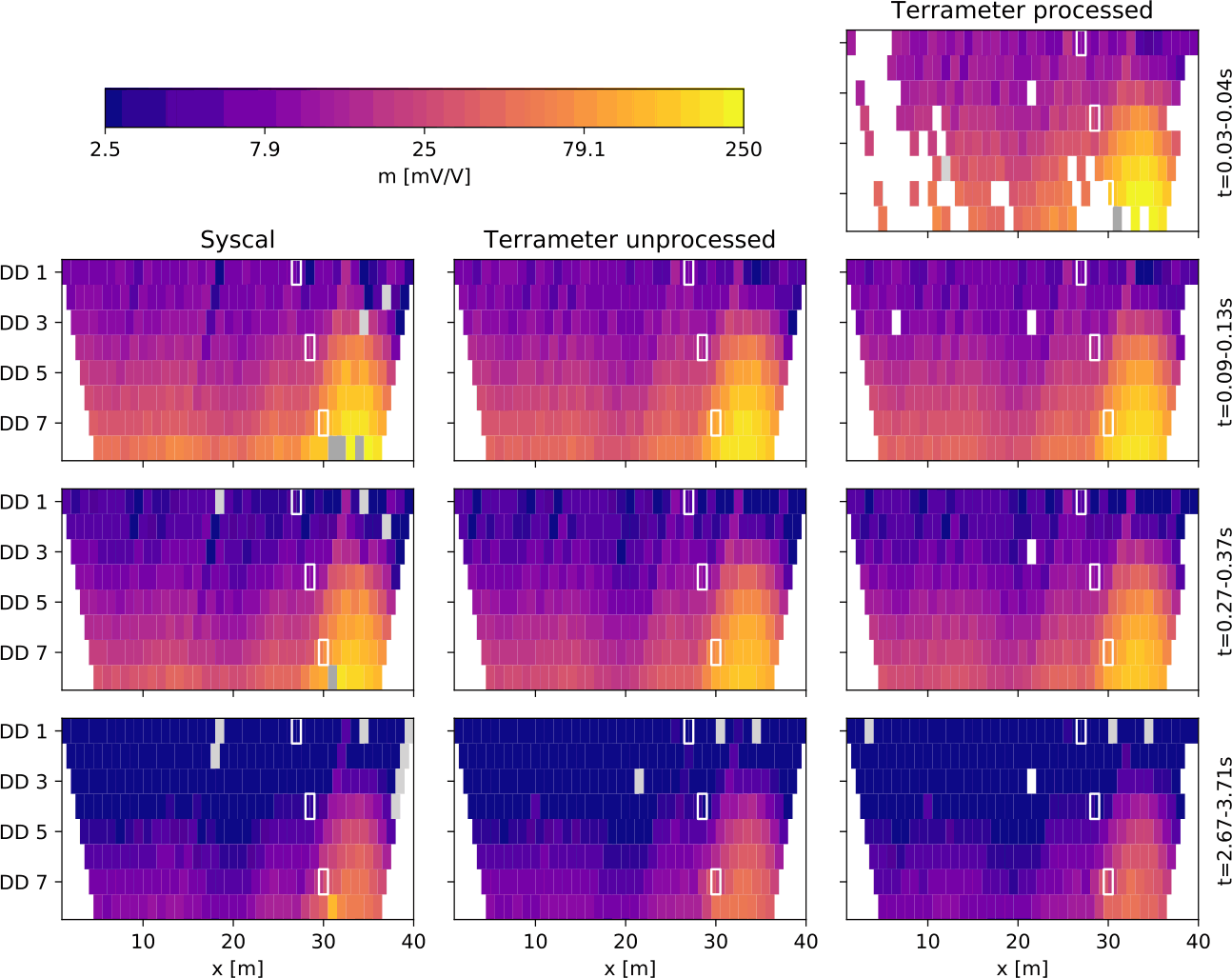
9.1.3 Inversion

Inversion (Martin u. a. 2020)

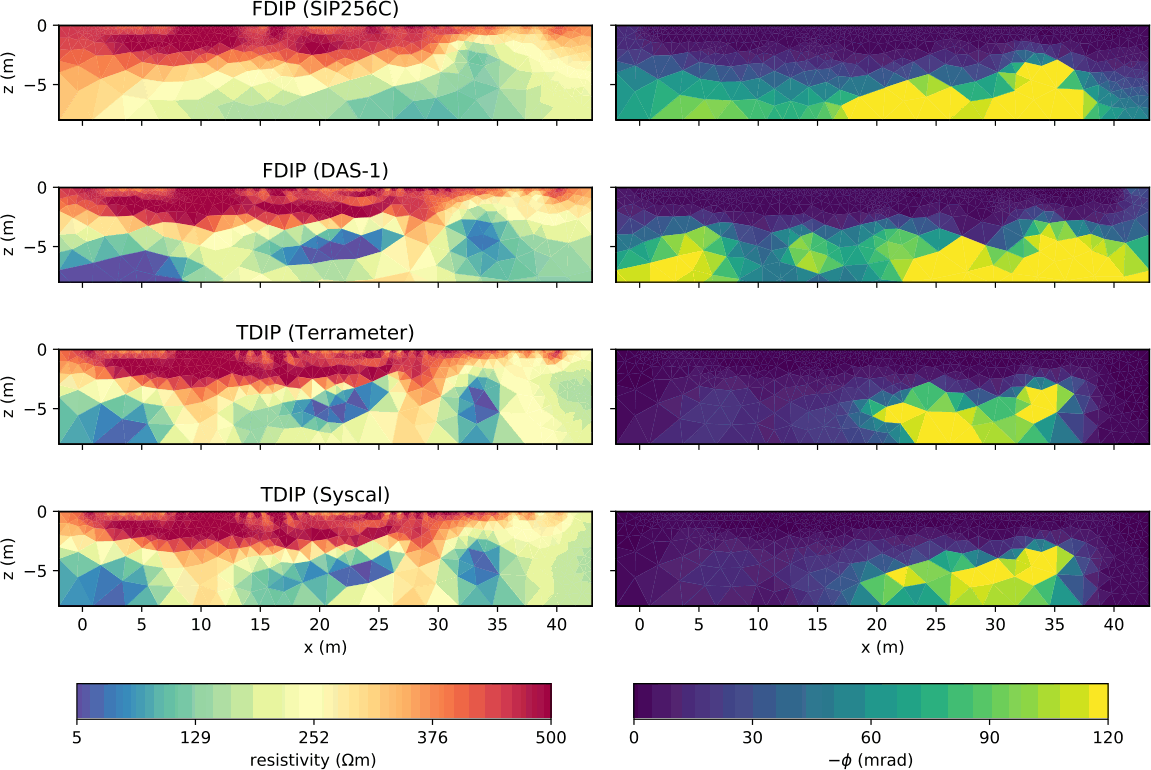
9.2 Umsetzung (Martin et al. 2021)

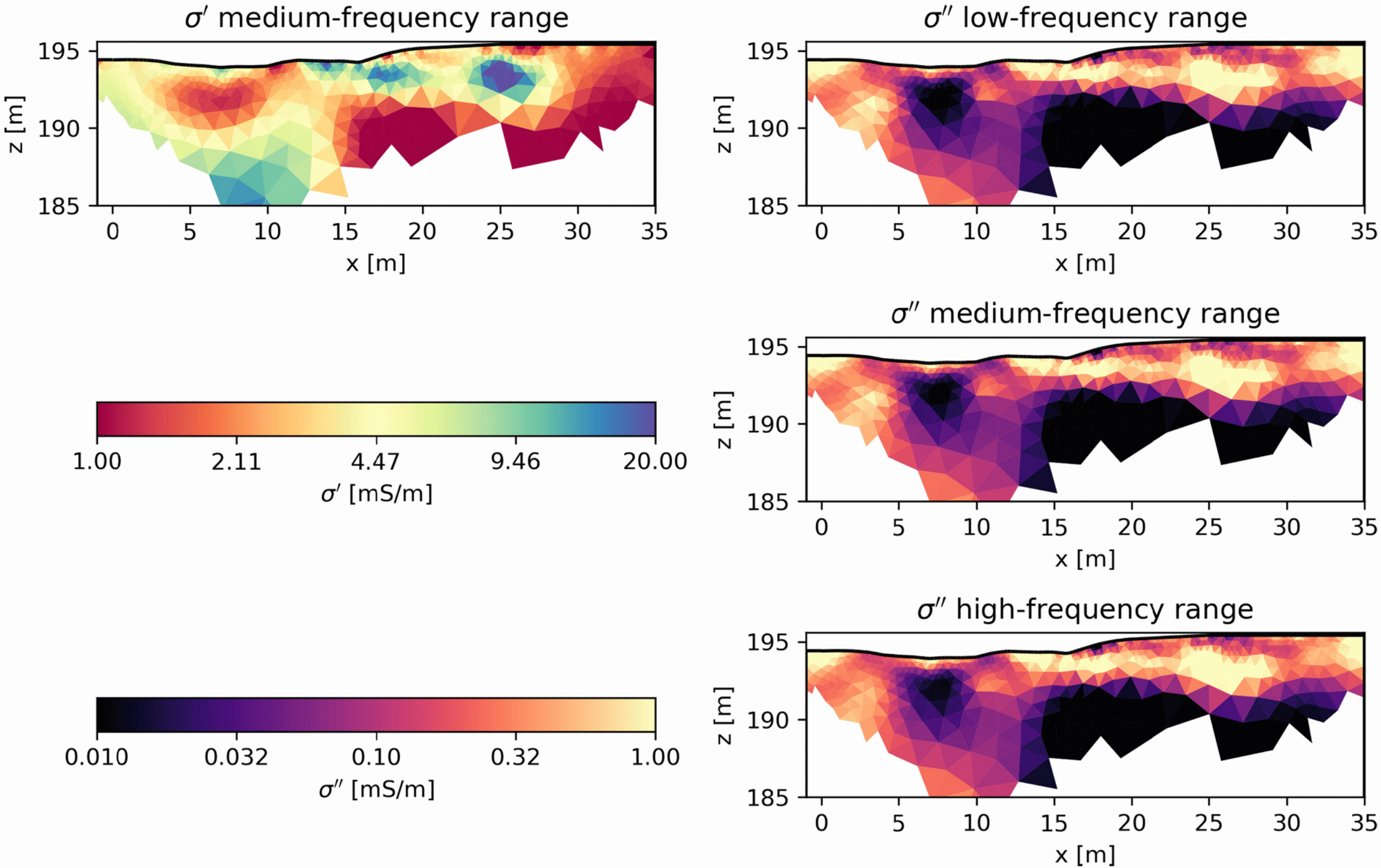
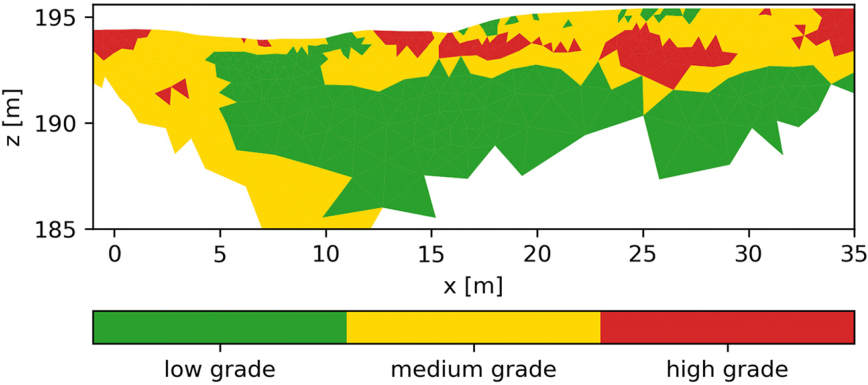
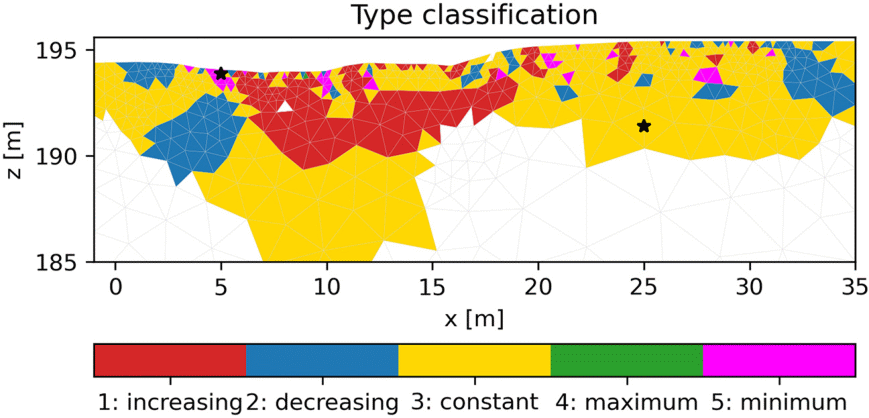
\(\Rightarrow\) Mineral-Grad/Typ

Abbildung 9.1: Inversionsergebnisse und Ableitung von Mineralgehalt und Typ (Martin u. a. 2021)