3 Grundgleichungen
3.1 Kontinuitäts-Gleichung
Für die stationäre Näherung (keine Zeitableitungen der Felder) ergibt sich aus den Maxwell-Gleichungen (Amperesches Durchflutungsgesetz) und dem ohmschen Gesetz \[\curl \vb H = \vb j = \sigma \vb E + \vb j_s\]
Dabei setzt sich die Stromdichte aus einem Anteil des im Untergrund (aufgrund der Leitfähigkeit \(\sigma\)) und einem Quellstromterm \(\vb j_s\) zusammen. Wir bilden die Divergenz der letzten Gleichung, und nutzen die Divergenzfreiheit von Wirbelfeldern (\(\div\curl\vb F=0\)):
\[\div \curl\vb H = \div\vb j=\div(\sigma\vb E) + \div\vb j_s=0\]
Daraus ergibt sich die Kontinuitätsgleichung:
\[-\div(\sigma\vb E)=-\div(\sigma\grad U)=\div\vb j_s\]
Diese partielle Differential-Gleichung (PDE) ist eine Poisson-Gleichung & beschreibt die Potentialverteilung für beliebige Verteilungen der Leitfähigkeit \(\sigma\). Im Allgemeinen lösen wir sie numerisch, für einfache Fälle analytisch.
3.1.1 Das Konzept der Punktquelle
Wir gehen zunächst von einer punktförmigen Einspeisung des Stroms aus.

Elektroden sind “klein” (gegenüber Abstand zu Potentialmessung), der Gesamt-Strom (Integral) beträgt \(I\):
\[\div\vb j = I \delta(\vb r - \vb r_s)\]
Daraus ergibt sich unendliche Stromdichte bei \(\vb r_s\) und \(\int\div\vb j=I\).
In Wirklichkeit sind Elektroden ausgedehnt und benötigen eine endliche Fläche, um den Strom durch eine endliche Stromdichte einzuleiten. Zum Beispiel kann man die Elektrode durch eine Kugel- oder Ellipsen-Form beschreiben:

3.1.2 Lösung für homogenen Vollraum
Für eine konstante Leitfähigkeit \(\sigma_0\) ist die Lösung der Kontinuitätsgleichung
\[-\div(\sigma_0\grad u)=\div \vb j_s\]
im Vollrau, dass sich der Strom radial auf die Oberfläche einer umgebenden Kugelschale mit dem Radius \(r\) verteilt
\[j=I/A=I/(4\pi r^2)\]
Damit ergibt sich für das Potential (Weg-Integral über das elektrische Feld) die Lösung
\[u(r)=r E=r j / \sigma = \frac{I}{4\pi\sigma r}= \frac{\rho I}{4\pi r}\]
Umgeformt nach \(\rho\), ergibt sich die Berechnung des (scheinbaren) spezifischen Widerstands \(\rho_a\) aus \(u\) und \(I\)
\[\rho_a = \frac{U}{I} 4\pi r = R\cdot k \quad\mbox{mit}\quad k=4\pi r\]
\(k\) wird als Geometrie-Faktor bezeichnet.
3.1.3 Formelle Lösung
Die Laplace-Gleichung in einem kugelsymmetrischen Koordinatensystem lautet
\[\laplacian u = \pdv[2]{u}{r} + \frac{2}{r}\pdv{u}{r}=0\]
Integration liefert \(\pdv{u}{r}=\frac{C_1}{r^2}\) und dann \(u=-\frac{C_1}{r} + C_2\)
Wegen \(u(r\rightarrow\infty)=0\) gilt \(C_2\)=0
\(I=4\pi r^2 j=-4\pi r^2 \sigma\pdv{u}{r}=-4\pi\sigma C_1 \quad\Rightarrow\quad u=\frac{I\rho}{4\pi r}\)
3.1.4 Lösung für homogenen Halbraum
Häufig finden geoelektrische Messungen auf der Erdoberfläche statt. Dann verteilt sich der Strom radial über die Halbkugel-Oberfläche
\[j=I/A=I/(2\pi r^2)\]
\[U(r)=r E=r \rho j=\rho I / (2\pi r)\]
und der (scheinbare) spezifische Widerstands aus \(U\) und \(I\)
\[\rho = \frac{U}{I} 2\pi r=R\cdot k \quad\mbox{mit}\quad k=2\pi r\]
Der Geometriefaktor \(k\) für eine Pol-Pol-Messung (Messung des Potentials gegen Unendlich und Stromeinspeisung gegen Unendlich) auf der Halbraumgrenze ist damit \(2\pi r\) wobei \(r\) der Abstand zwischen der Stromelektrode (A) und der Spannungsmessung (M) ist.
3.1.5 Zwei Strom-Elektroden
Für einen Stromkreis wird eine zweite, negative, Elektrode (B) benötigt. Von einer Pol-Messung spricht man auch, wenn B sehr weit weg von der Spannungsmessung ist. In der Praxis sind diese Messungen aber selten, da man dafür ein langes Kabel zur Elektrode B benötigt.
Durch Überlagerung der Potentiale der positiven Elektrode A und negativen Elektrode B ergibt sich das Potential \[u(\vb r) = \frac{I\rho}{2\pi} \Big(\frac{1}{|\vb r - \vb r_A|}-\frac{1}{|\vb r - \vb r_B|} \Big)\]
Theoretisch könnte man zwischen A und B sowohl Strom als auch Spannung messen und damit \(\rho\) bestimmen. Zum einen ist es aber schwer, da über das Strommessgerät eine Spannung abfällt oder über das Spannungsmessgerät ein Strom fließt. Zum anderen würde man neben dem Untergrundwiderstand \(R_E\) noch die Ankopplungs-(Übergangs)-Widerstände an den Elektroden (\(R_A\) bzw. \(R_B\) messen).

Daher verwendet man in der Regel getrennte Strom- und Spannungselektroden. Das Potential an der Elektrode M muss auch gegen ein anderes Potential (Elektrode N) gemessen werden. Auch diese kann weit weg (im Unendlichen) liegen, womit sich eine Pol-Pol-Messung ergibt, meist messen wir aber auf einer endlichen Strecke.

3.1.6 Konfigurations/Geometrie-Faktor
Das Potential an der Elektrode M aufgrund Stromeinspeisung in A beträgt \(u_{AM} = \rho I \frac{1}{2\pi \overline{AM}}\), ensprechend \(u_{AN} = \rho I \frac{1}{2\pi \overline{AN}}\), \(u_{BM} = \rho I \frac{1}{2\pi \overline{BM}}\) und \(u_{BN} = \rho I \frac{1}{2\pi \overline{BN}}\). Die gemessene Spannung \(U\) ergibt sich aus der Überlagerung der Potentiale unter Berücksichtigung der Vorzeichen
\[ U = u_{AM} - u_{AN} - (u_{BM} - u_{BN}) \]
\[ U = \rho I \big( \frac{1}{2\pi \overline{AM}} - \frac{1}{2\pi \overline{AN}} - \frac{1}{2\pi \overline{BM}} + \frac{1}{2\pi \overline{BN}}\big)\]
Durch Umformung ergibt sich für den Widerstand \[ \rho = \frac{U}{I} k \quad\mbox{mit}\quad k = \frac{2\pi}{\frac{1}{\overline{AM}}-\frac{1}{\overline{AN}}-\frac{1}{\overline{BM}}+\frac{1}{\overline{BN}}} \]
Dies gilt nur für ein homogenes Medium, im Allgemeinen kann diese Formel aber immer verwendet werden und es ergibt sich ein so-genannter scheinbarer spezifischer Widerstand (engl. apparent resistivity) \(\rho_a\), der den spezifischen Widerstand für einen äquivalenten Untergrund angibt.
3.1.7 Stetigkeit an Grenzflächen
Bisher sind wir von homogenen Medien ausgegangen, die zu linearen Stromlinien und kugelförmigen Potentiallinien führen. An einer Grenzfläche zwischen zwei spez. Widerständen \(\rho_1\) und \(\rho_2>\rho_1\) weichen Potential und die Stromlinie davon ab.

Aus der Kontinuitätsgleichung \[\div(\sigma\vb E)=-\div(\sigma\grad u)=0\] ergeben sich Stetigkeitsbedungen:
- das Potential ist stetig
- die Normalkomponente der Stromdichte ist stetig \(j_{z1}=j_{z2}\)
- die Tangentialkomponente des elektrischen Feldes ist stetig: \(E_1=E_2\Rightarrow \rho_1 j_{x1}=\rho_2 j_{x2}\)
Dividiert man beide Gleichungen, erhält man
\[\rho_1 \frac{j_{x1}}{j_{z1}}=\rho_2 \frac{j_{x2}}{j_{z2}}\]
bwz. \(\rho_1\tan\theta_1=\rho_2\tan\theta_2\) das Brechungsgesetz:
\[\frac{\tan\theta_2}{\tan\theta_1}=\frac{\rho_1}{\rho_2}=\frac{\sigma_2}{\sigma_1}\quad. \]
3.1.8 Verhalten an Grenzflächen
Betrachten wir eine Grenzfläche zwischen zwei Schichten mit Faktor 10 verschiedener Leitfähkeitkeit, einmal mit Einspeisung im guten Leiter und einmal im schlechten Leiter:
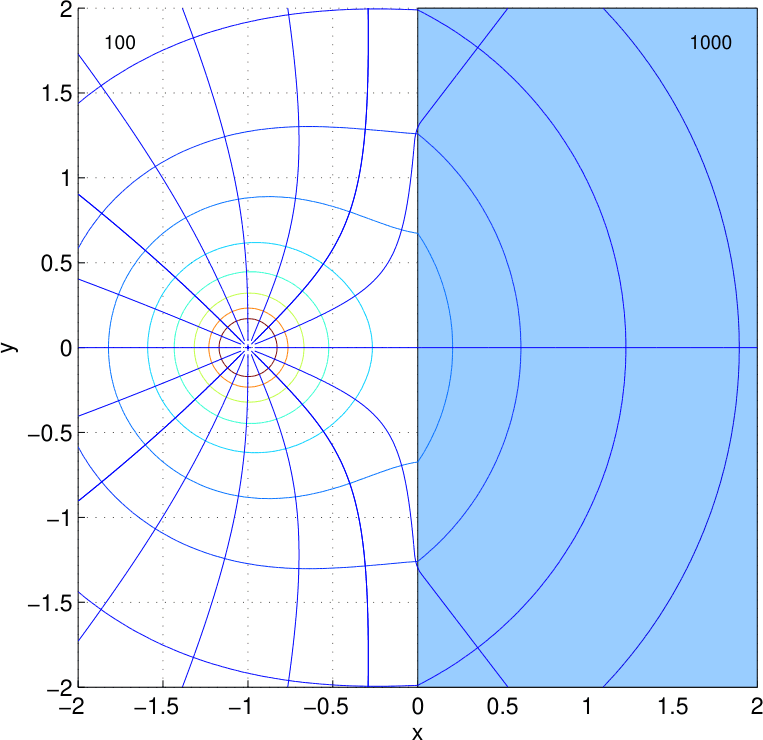
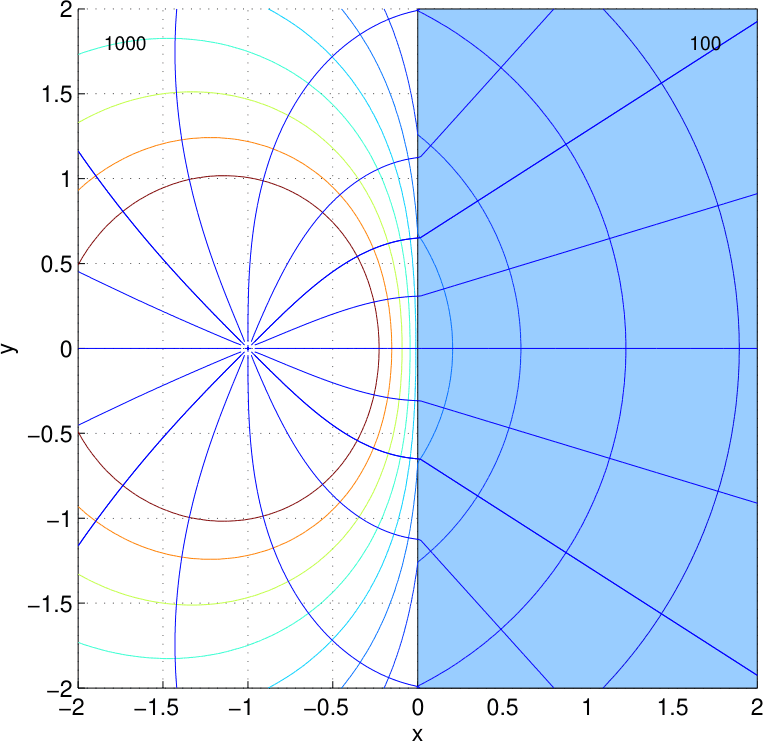
Die Stromlinien werden zum schlechten Leiterhin und vom guten weg gebrochen, während die Potentiallinien im schlechten Leiter mehr Raum einnehmen und sich im Übergang zum guten Leiter hin verdichten.
3.2 Feldausbreitung
Wir studieren nun die Potentialverteilung für Oberflächenmessungen, zunächst für ein homogenes Medium
Dabei überlagern sich die kreisförmigen Potentiale der Stromelektroden mit verschiedenem Vorzeichen, so dass in der Symmetrielinie eine Nullinie ergibt. Die Stromlinien ergeben sich als Gradienten des Potentials:
Wir bauen nun in einer Tiefe von 2m einen schlechten Leiter ein:
und sehen, dass die Stromlinien oberhalb sich parallel zur Grenzfläche ausbilden, während das Potential im schlechten Leiter verstärkt.
Wenn wir die Leitfähigkeiten vertauschen,
beobachten wir, dass die Stromlinien zum guten Leiter hingezogen werden und in diesem eher horizontal fließen.
3.2.1 Inhomogener Untergrund
Für einen allgemeinen inhomogenen Untergrund
ist das Stromsystem komplexer:
Auch hier wird der Stromfluss vom guten Leiter eingezogen und vom schlechten Leiter verdrängt. Dabei wird die Null-Potentiallinie in Richtung des Schlechten Leiters verdrängt. Hier ist aber die Lage der Anomalien von Bedeutung. Wie genau Leitfähigkeits-Änderungen das Potentialfeld und damit die Messung verändern, wird mit dem Begriff Sensitivität beschrieben.