11 Grundgleichungen
- Maxwellgleichungen
- Feldgrößen der Elektromagnetik
- Materialgleichungen, Ohmsches Gesetz
Feldgrößen werden im Zeitbereich als Funktion des Ortes und der Zeit gemessen, z.B.
\[ \mathbf{e} = \mathbf{e}(\mathbf{r}, t). \]
Bei Verfahren mit Wechselfeldern kann die explizite Zeitabhängigkeit durch eine Fouriertransformation abgekoppelt werden.
Im Zeitbereich werden die Feldgrößen kleingeschrieben, z.B. \(\mathbf{e}\), \(\mathbf{h}\).
Im Frequenzbereich schreiben wir die Feldgrößen mit Großbuchstaben, z.B. \(\mathbf{B}\).
Der Zusammenhang wird durch die Fouriertransformation hergestellt:
\[ \begin{align} f(t) & = \frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{ +i \omega t }\, \mathrm d \omega \\ F(\omega) & = \phantom{\frac{1}{2 \pi}} \int_{-\infty}^{\infty} f(t) e^{ -i \omega t }\, \mathrm d t \end{align} \]
Die Zeitabhängigkeit wird durch den Term \(e^{ i \omega t }\) eingeführt, und wir schreiben \[ \mathbf{E}(\omega) = \mathbf{E}_{0} e^{ i \omega t }. \] Der Term \(e^{ i \omega t }\) tritt bei allen Feldgrößen als derselbe Faktor auf und wird daher der besseren Übersicht halber weggelassen.
Die physikalisch relevante Größe ist die Feldamplitude \(\mathbf{E}_{0}\).
11.1 Maxwell-Gleichungen
11.1.1 Zeitbereich
\[ \begin{align} \curl \mathbf{h} & = \mathbf{j} + \frac{ \partial \mathbf{d} }{ \partial t } \qq{Ampere} \\ \curl \mathbf{e} & = -\frac{ \partial \mathbf{b} }{ \partial t } \qq{Faraday} \\ \div \mathbf{b} & = 0 \qq{Gauß} \\ \div \mathbf{d} & = \rho_{E} \end{align} \]
11.1.2 Frequenzbereich
\[ \begin{align} \curl \mathbf{H} & = \mathbf{J} + i \omega \mathbf{D} \qq{Ampere} \\ \curl \mathbf{E} & = -i \omega \mathbf{B} \qq{Faraday} \\ \div \mathbf{B} & = 0 \qq{Gauß} \\ \div \mathbf{D} & = \rho_{E} \end{align} \]
11.2 Materialgleichungen
\[ \begin{align} \mathbf{b} & = \mu \mathbf{h} \\ \mathbf{d} & = \varepsilon \mathbf{e} \end{align} \]
bzw. \[ \begin{align} \mathbf{B} & = \mu \mathbf{H} \\ \mathbf{E} & = \varepsilon \mathbf{E} \end{align} \]
11.3 Ohmsches Gesetz
\[ \mathbf{j} = \sigma \mathbf{e} \quad\text{ bzw. }\quad \mathbf{J} = \sigma \mathbf{E}. \]
11.4 Schematisches Konzept der elektromagnetischen Induktion
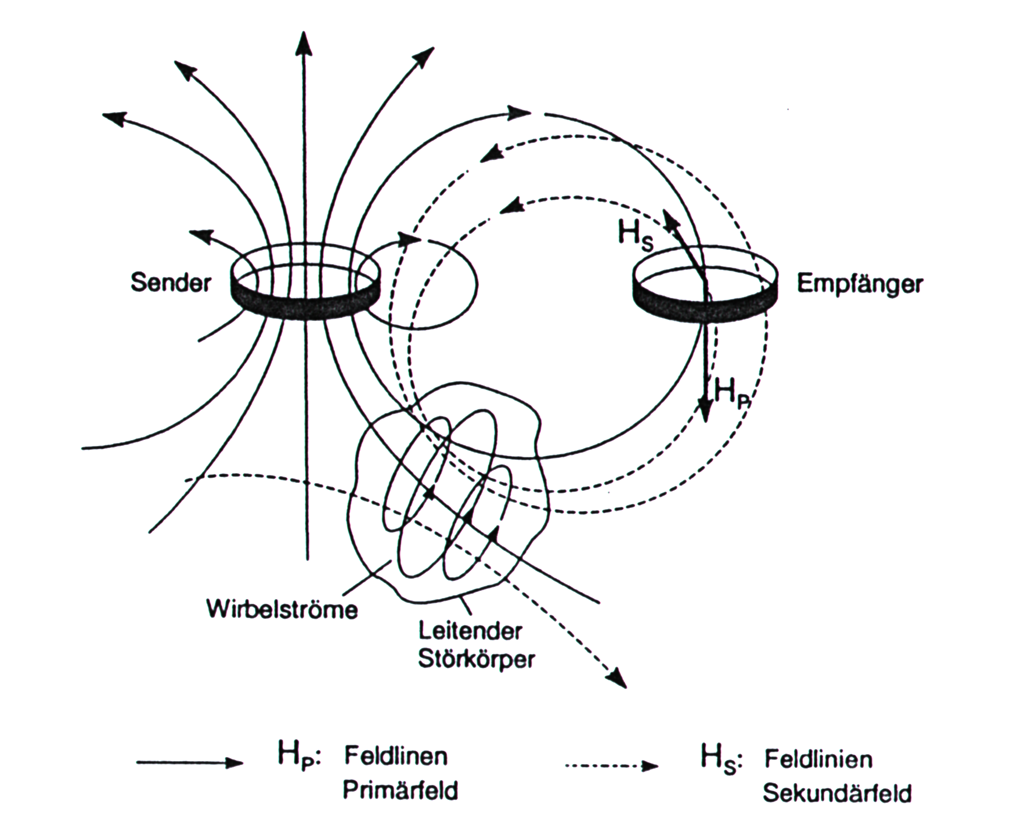
Faradaysches Induktionsgesetz \(\to\) Ohmsches Gesetz \(\to\) Amperesches Durchflutungsgesetz
Das sekundäre Magnetfeld ist gegenüber dem primären Magnetfeld phasenverschoben und hat eine geringere Amplitude.
Über Amplitude und Phasenverschiebung lassen sich die Leitfähigkeit und die Geometrie des Störkörpers unter Beachtung des Äquivalenzprinzips rekonstruieren.
11.5 Felder und Einheiten
| Name | Symbol | Einheit |
|---|---|---|
| Magnetfeld | \(\mathbf{H}\) | A/m |
| Elektrisches Feld | \(\mathbf{E}\) | V/m |
| Magnetische Flussdichte | \(\mathbf{B}\) | Vs/m\(^{2}\) (T) |
| Dielektrische Verschiebung | \(\mathbf{D}\) | As/m\(^{2}\) |
| Elektrische Stromdichte | \(\mathbf{j}\) | A/m\(^{2}\) |
| Spannung | \(U\) | V |
11.6 Messgrößen
| Name | Symbol | Messgerät |
|---|---|---|
| Elektrisches Feld | \(\mathbf{E}\) | Elektroden |
| Magnetische Flussdichte | \(\mathbf{B}\) | Magnetometer |
| Zeitliche Änderung der Flussdichte | \(\frac{ \partial \mathbf{B} }{ \partial t }\) | Induktionsspulen |
Mit Induktionsspulen kann nur die zeitliche Änderung der magnetischen Flussdichte als induzierte Spannung gemessen werden: \[ U_{ind} \sim \frac{ \partial \mathbf{B} }{ \partial t } \]
11.7 Einteilung der Methoden nach Merkmalen der Felder
| \(\nabla \times \mathbf{H}=\) | \(\nabla \times \mathbf{E}=\) | |||
|---|---|---|---|---|
| Wellenvorgänge | \(\mathbf{j} + \frac{ \partial \mathbf{D} }{ \partial t }\) | \(- \frac{ \partial \mathbf{B} }{ \partial t }\) | GPR | HF-Methoden |
| Quasistationäre Vorgänge | \(\mathbf{j}\) | \(- \frac{ \partial \mathbf{B} }{ \partial t }\) | CSEM, MT, TEM | NF-Methoden |
| Stationäre Felder | \(\mathbf{j}\) | \(\mathbf{0}\) | Geoelektrik | DC |
| Statische Felder | \(\mathbf{0}\) | \(\mathbf{0}\) | – |
11.8 Messung
Bei der Messung wird versucht, die Übertragungsfunktion oder response function des Systems Erde zu erfassen.
Dazu ist ein breites Frequenzspektrum erforderlich.
Input \(\to\) Erde \(\to\) Output
\(\ \ \mapsto\)
Feld \(\to\) Erde \(\to\) Feld